【LinearAlgebra】선형대수 정리 1 (한글강의)

in Self Study

쑤튜브 선형대수 강의내용 정리 1강~22강

youtube 강의 링크 : 쓔튜브 선형대수 강의 링크

1강~5강까지는 매우 기초적인 내용이라 정리하지 않았습니다.

6강 Systems of linear equations

  1. 확장 행렬(Augmented matrix)이란? 선형연립방정식을 행렬로 표현한 것.

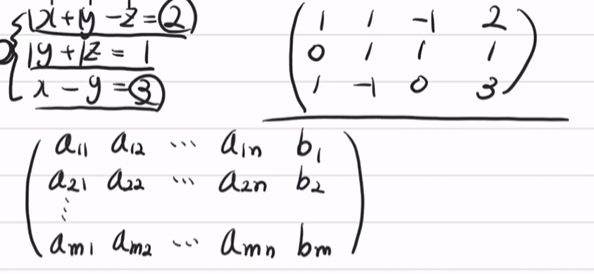
    image-20201111204926141

  2. reduced row echelon form (기약 행 사다리꼴)

    • 해가 이미 구해진 형태의 확장 행렬
    • x3 = 2라고 한다면 확장행렬의 한 row는 0 0 1 2가 될 것이다.
    • 아래의 4가지 규칙을 만족할 때 reduced row echelon form이라고 부를 수 있다.
      1. 영 행이 아니라면, 각 행에서 처음 등장하는 영이 아닌 수는 1이고, 이를 leading 1이라고 부른다.
      2. 영행은 항상 맨 아래에 모여있다.
      3. leading 1의 위치는 항상 한 칸 이상 뒤로 밀린다.
      4. leading 1이 포함된 열은 leading 1을 제외하면 모두 0이다.

Gauss Jordan Elimination (7강)

  • 일반적인 연립선형의 확장행렬을 reduced row echolon form(기약행사다리꼴)으로 바꿔주는 방법

    1. Elementary row operations(기본 행 연산)

      • 한 행에 상수배(=! 0) 하는 방법
      • 한 행의 상수배(=! 0)를 다른 행 더하기
      • 행 교환

    2. 가오스 소거법

      확장행렬을 기약 행 사다리꼴(row echelon = leading 1 아래로 0인 행렬)로 바꾸는 알고리즘

      • (1행부터 아래로) 기본 행 연산을 통해서 행 사다리꼴을 만들어 주는 과정
      • leading1 앞을 0으로 만들어주는 과정
      • 여기까지는 가오스 소거법이다.

    3. reduced (기약) 형태(leading1 뒤도 0인 행렬) 만들어 주기

      • 이게 가오스 조던 소거법이다.
      • (마지막행부터 위로 back substitution) 기본 행 연산을 통해서 기약(reduced) 행 사다리꼴을 만들어 주는 과정

  • 이 알고리즘을 통해서 컴퓨터로 해를 구하는 과정이 매우 쉬워졌다. 가감법 대입법을 사용해서 해를 구하면 엄청 오래 걸린다.

  • (8강 Gauss Jordan Elimination의 고찰) 가오스 조던 소거법은 왜 가능할까? 가오스 소거법이 연립 일차방정식의 가감법이다. 가오스 조던 소거법이 연립 일차방정식의 대입법이다.

행렬의 기본 연산과 이론

  • 13강 Identity matrix (항등행렬) - 행렬의 곱샘 항등원이다.

  • 14강 역행렬(inverse matrix, invertable (역행렬 존재하는 행렬=가역행렬))

    • 곱샘의 항등원에 대한 역원)
    • 귀류법을 이용한 증명에 의해, 한 행렬의 역행렬은 유일하다 (1개만 존재한다).
    • 영인자(zero divisor) - 0이 아닌 두 행렬을 곱해서 0이 나올 수 있다.
    • 가오스 조던 소거법을 이용한 역행렬 구하는 방법
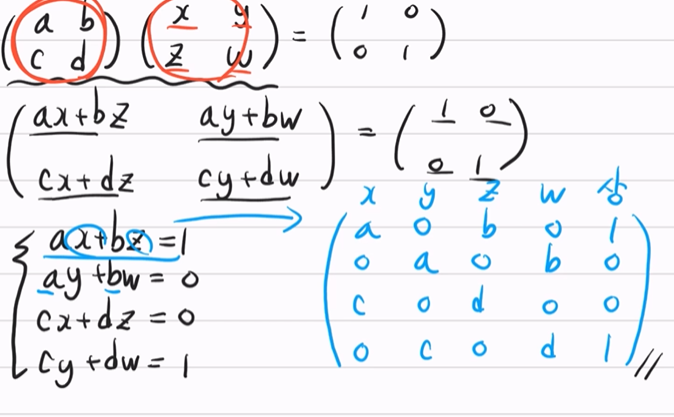
      • image-20201113213128976
      • 파랑색 행렬에 대해서, 가오스 조던 소거법을 사용해 x,y,z,w를 구하면 우리에게 익숙한 2차 정사각행렬의 역행렬 공식을 구할 수 있다.

  • 15강 역행렬의 성질

    • invertable (역행렬 존재하는 행렬=가역행렬)을 판단하는 방법? determinent(행렬식)=0 인지를 판단
    • non-invertible한 행렬? singular matrix. determinent(행렬식)=0인 metrix
    • 역행렬의 지수곱. 역행렬의 역행렬은 자기자신. 스칼라배는 역수.
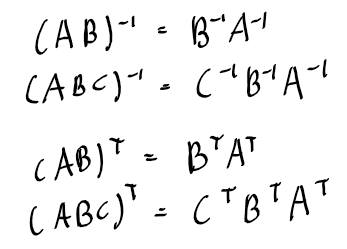
    • image-20201113222625212

  • 16강 전치행렬(transposed matrix)

    • 덧셈의 분배법칙 성립. (모든 증명은 동영상에 있다)
    • 곱셉의 분배법칙은 위와 같이 위치가 뒤바껴야 한다.
    • A가 invertable이면 transe(A)도 invertable이다.
    • inverse(trace(A)) = trace(inverse(A)) 이다.

  • 17강 대각합(trace)

    • n차 정사각행렬 A에 대해서, 대각성분들의 합을 대각합이라 한다.
    1. dot product와 행렬곱 사이의 관계
      • 열백터 -> 백터로 취급 가능하다.
      • dot product( • ) - 백터와 백터, 열백터와 열백터 (EX. (AB)ij => transe(Ai) • (Bj))
      • A : nxn, (n,v는 열백터) u : nx1, v : nx1 일때, Au • v = u • transe(A)v , u • Av = transe(A)u • v

기본 행렬과 가역행렬의 관계

  • 18강 기본행연산의 행렬화 (강의 꼭 한번 더 보기)

    • 열백터 -> 백터로 취급하기
      • 열백터의 행교환 = 백터의 좌표 뒤바꿈 -> 선형변환=선형사상(linear transformation) -> 이 변환식을 행렬로 표현(행렬화)할 수 있다.
        • 선형사상은 행렬로 표현할 수 있다.
        • 기본행 연산도 행렬로 표현할 수 있다.
      • y = f(x)의 함수로써 그 함수가 열백터의 행을 바꾸는 함수하면, 그 함수의 확장행렬은 아래와 같다.
      • image-20201113225645176
      • 즉 열백터의 행교환을 하고 싶으면 I의 행교환 시킨 행렬을 곱해주면 되고
      • 행렬 행백터의 열교환을 하고 싶으면 I의 열교환 시킨 행렬을 곱해주면 된다.
      • 스칼라곱을 하는 linear transformation으로, 한 행에 상수배를 해주고 싶으면, I의 i행에 상수배를 한 행렬이 변환행렬이다. (행렬화)
      • 이와 같은 기본 행연산(행변환, 열변환, 상수배, 행or열이 일차 결합)을 행렬화 할 수 있다. = 기본행렬

  • 19강 기본행렬(elementary matrix)과 기약행사다리꼴의 역행렬

    • 기본행렬 - 1. 행교환 2. 행의 상수배 3. 행의 상수배를 다른 행의 더하기. 이러한 역할을 하는 행렬을 의미한다. 이 3가지 역할 중 2개 이상을 수행하는 행렬은 기본행렬이라고 하지 않는다.(기본행렬 2개를 곱해주면 2개의 역할을 수행할 수 있긴 하지만. 그렇게 곱해서 나온 행렬은 기본행렬이라 하지 않는다.)
    • 기본행렬의 특징
      • n차 정사각행렬.
      • 선형사상이다(정의역과 치역의 Space가 동일하다. 다르거나 일부분이라면 선형사상이 아니다.) = 기본행렬은 항상 가역행렬이다. = 역행렬이 항상 존재 한다.
      • 항상 항등행렬을 이용해서 만든다(18강 처럼) = 그렇다면 그 행동과 완전히 반대대는 역할을 하는 행렬이 당연히 반드시 존재할 것이다. (ex, I의 i행과 j행을 행교환한 행렬 <-> I의 j행과 i행을 행교환한 행렬) 즉! 역행렬이 항상 존재한다.
    • 기약행사다리꼴 중 영행을 포함하는 행렬은 determinent=0 이다.(증명 나중에) 따라서 기약행사다리꼴 중 역행렬이 존재하는 행렬은 단위행렬 뿐이다.
    • 따라서! A가 가역행렬(역행렬이 존재하면)이면 A를 가오스 조던 소거법을 행하여 구한 기약행사다리꼴은 단위행렬이다!! = A에 가오스 조던 소거법을 적용하는 것이, “기본행렬 연산을 여러번 수행”하는 것이다. 따라서 A의 역행렬이 존재한다면, A에 가오스 조던 소거법을 취하면 단위행렬 형태가 되고, A의 역행렬은 위에서 적용한 “기본행렬 연산의 여러번 수행”이 역행렬 그 자체이다.

  • 20강 분할행렬과 역행렬 알고리즘

    • n차 정사각행렬 A에 대해서

    • 위의 명제의 역도 성립한다. A의 (가오스 조던 소거법을 적용해 구한) 기약행렬사다리꼴이 I라면, A는 가역행렬이다.

    • 이때 나오는 명제는 이것이다. A가 역행렬이 존재하면, A는 기본행렬들의 곱으로 표현가능하다.

    • 따라서 삼각형으로 연결된 3개의 명제는 서로서로 필요충분조건이다. 서로 동치(사실상 같은 말)이다.

    • image-20201115194429022

    • 행동치(row equivalent)를 이용한 A의 역행렬 구하기

      • Ek x … x E2 x E1 (기본 행 연산들) x A = B 에서 A와 B는 행동치이다.

        • = A에서 기본행 연산을 몇개 수행하면 B가 나온다
        • = B에서 기본행렬산을 몇개 수행하면 A가 나온다.

      • A와 I는 행동치이다.

        • = A에서 기본행 연산의 곱으로 표현가능하다.
        • = A는 가역이다.
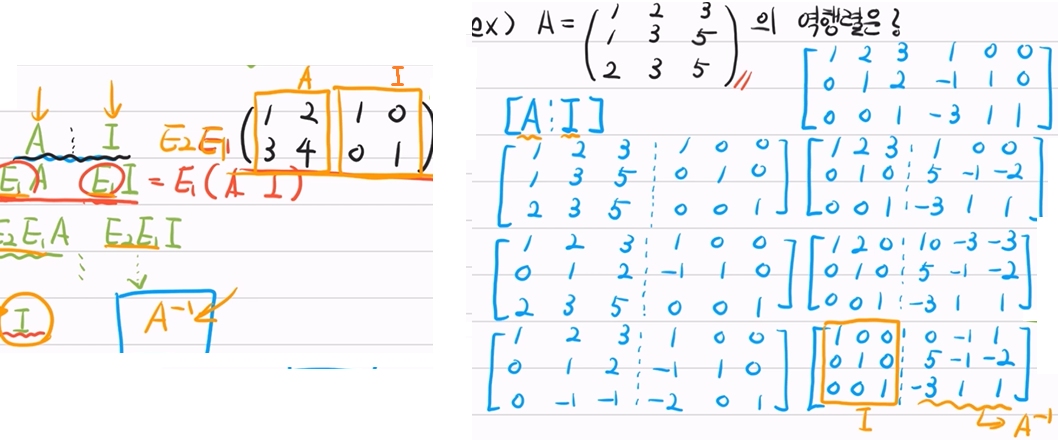
        • 결론 : A와 I가 행동치이면, A를 항등행렬로 바꿔주는 “기본행 연산의 행렬들을” 그대로 항등행렬에 곱해주면, A의 역행렬이 나온다
        • A = Ek x … x E2 x E1 (기본 행 연산들) 일 때,
          • Ek x … x E2 x E1 (기본 행 연산들) x inverse(A) = I
          • I x inverse(A) = inverse( Ek x … x E2 x E1 (기본 행 연산들) ) x I 이므로, 아래와 같이 하면 된다.
        • 블록행렬(분할행렬) = A의 역행렬 구하기
          1. Ek x … x E2 x E1 (기본 행 연산들) = 가오스 조던 소거법을 위한 기본행 연산들
          2. 이 연산들을 I에다가도 적용해 주기
          3. 따로따로 계산하지 말고 블록으로 묶어서 한번에 연산하기
          4. image-20201120124739888

연립선형방정식과 행렬의 관계

  • 21강 연립선형방정식과 행렬의 관계1
    • A x = B (nxn) (nx1) (nx1)
    • consistent : 해가 적어도 한 개가 있는 경우
    • inconsistent : 해가 전혀 없는 경우
    • homogeneous : 동차 연립선형방정식 (B=0인 경우. A에 역행렬이 존재하면 자명해 만을 가진다.)
  • 22강 연립선형방정식과 행렬의 관계2
    • 선형함수/선형사상 - ‘선형적인 곱과 덧셈으로만 이루어진 식’ 말고 수학적 정의
      1. 가산성 f(x+y) = f(x) + f(y)
      2. 동차성 a * f(x) = a * f(x)
    • 행렬연산: A(x+y) = Ax+Ay , A(ax) = aAx -> 선형 사상이다!
    • 연립성형방정식과 역행렬과의 관계
      • A x = B (nxn) (nx1) (nx1)
      • A가 가역이면(b!=0), 방정식의 해는 존재하고 유일하다. (유일해를 가진다)
        • Y는 x의 유일해.
        • augmented matrix(A:b) –가오스조던소거법–> (I:Y)
        • (위에 참조) A와 I는 행동치이다 = A는 가역행렬이다.
    • AB가 가역행렬이면 A와 B도 각각 가역행렬이다. (증명은 22강 참조)
      • 내가 만든 명제 : AB가 가역행렬이면, AB를 기본행연산들의 곱으로 표현가능하다. 그 기본행 연산들을 나눠서 한쪽을 A, 다른 한쪽을 B라고 할 수 있을 것이다. A와 B 또한 기본행 연산들의 곱이므로, 가역행렬이다.

© All rights reserved By Junha Song.