【Distribution】 Source-Free to Measurement Shift via Feature Restoration

Questions to the author

Q1) Why did you use softly-binned histograms as a approximation of soure feature?
Q2) Have you ever considered covariance matirix or feature statistics (mean&std) ? If you tried it already, Could you share some brief results?

we compared to both of them in the paper. See “Marg. Gauss [1]” and “Full Gauss [2]” baselines. Bins did better, and we used them because we observed bi-modal and skewed marginal activation distributions (as explained in the paper).
Refrence
- [1] Source-free domain adaptation via distributional alignment by matching batch normalization statistics. arXiv 2021
- [2] (저자 직접 실험) the distributions are aligned using the KL divergence DKL(Q||P) of the empirical mean vector and covariance matrix
답변을 참조해 논문 분석한 결과
- Marg. Gauss 보단 Full Gauss 이 좋다.
- Marg. Gauss, Full Gauss 모두 SF-DA 관점에서 성능을 올려주긴하지만, FR(feature restoration)과 BUFR(bottom-up feature restoration) 을 이기진 못한다. Accuracy와 ECE를 비교해봤을때 FR과 BUFR 성능이 훨씬 (1.5배 이상) 좋다.
- 하지만, Marg. Gauss는 Layer5 이후에 feature Restoration을 수행한다. Full Gauss는 어디에 적용하는지 나와있지 않다.
- BUFR에서는 [training for several epochs on one “block” before “unfreezing” the next] 라고 했다. 나도 이와 비슷한 방법을 사용해도 좋을 듯 하다. (30 epochs per block)

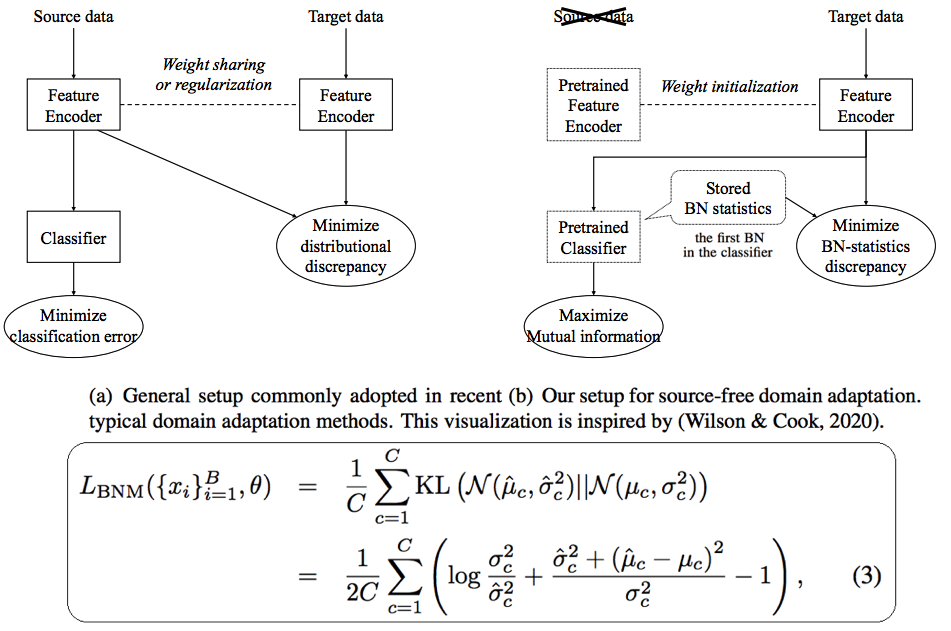
KL divergence를 선택한 이유는 2개의 Gaussian distributions를 비교 계산하기에 쉽고, 통계학적으로 자연스러운 계산이기 때문이다. (Ablation study가 적절하지 않으므로 이 말은 신뢰성이 없다. 어쨋든 2개의 Gaussian distributions 을 비교하는 가장 단순한 수식이 될 수 있겠다.)
실험 결과에 성능향상 정도를 보면, 매우 미약한 성능 향상을 볼 수 있다. 너무 높은 Layer에 style matching을 시켰던 것이 가장 큰 단점인듯 하다.