【LinearAlgebra】선형대수 정리 3 (한글강의)
in Self Study
쑤튜브 선형대수 강의내용 정리 45~86강. - 57강 행공간의 보존 ~ 74강까지 패스. 너무 수학적임 나한테 아직 필요 없음
- 나중에 꼭 들어야 하는 강의 -71강 : k < n, k개의 정규기저백터에서, n-k개의 추가 정규기저백터 찾기
-72강 : 블록행렬. 내가 만든 열=다열, 행=행다 개념을 블록으로 설명하는 강의.
youtube 강의 링크 : 쓔튜브 선형대수 강의 링크
Matric 내적 정리 요약
- 블록행렬 강의를 한번 보면 좋을 듯. 하지만 우선 아래는 내가 만든 공식

Basis & Dimension
- 45강, 46강 기저와 차원
- 기저 백터의 조건
- 선형적으로 독립
- n차원이면 n개의 백터 이상.
- 47강 기저 변환
- E = {e1,e2,e3 … en} -> V = {v1,v2,v3 … vn} | e1과 v1은 백터 | v끼리는 서로 정규일 필요는 없다.
- 아래에서 x(kn) 은 V의 원소들의 선형결합 계수 이다.
- xk1v1 * xk2v2 * xk3v3 * … xknvn = ek | k = 1~n까지 n차 연립방정식
- 위의 n개의 연립방정식으로 행렬로 표현하면 아래와 같다.
- 정리 :

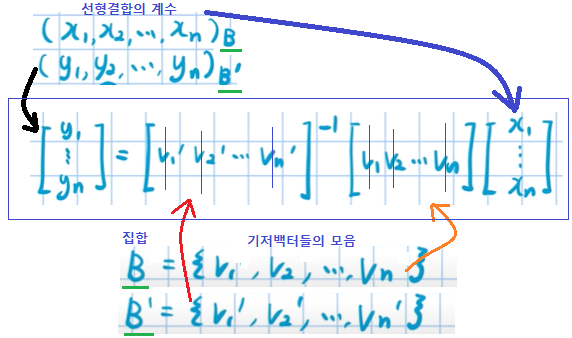
- 일반화 (48강에서 증명)
- (x1,x2 … xn)B = B의 기저백터들에 x1,x2,x3..xn의 계수로의 선형결합
- 예시
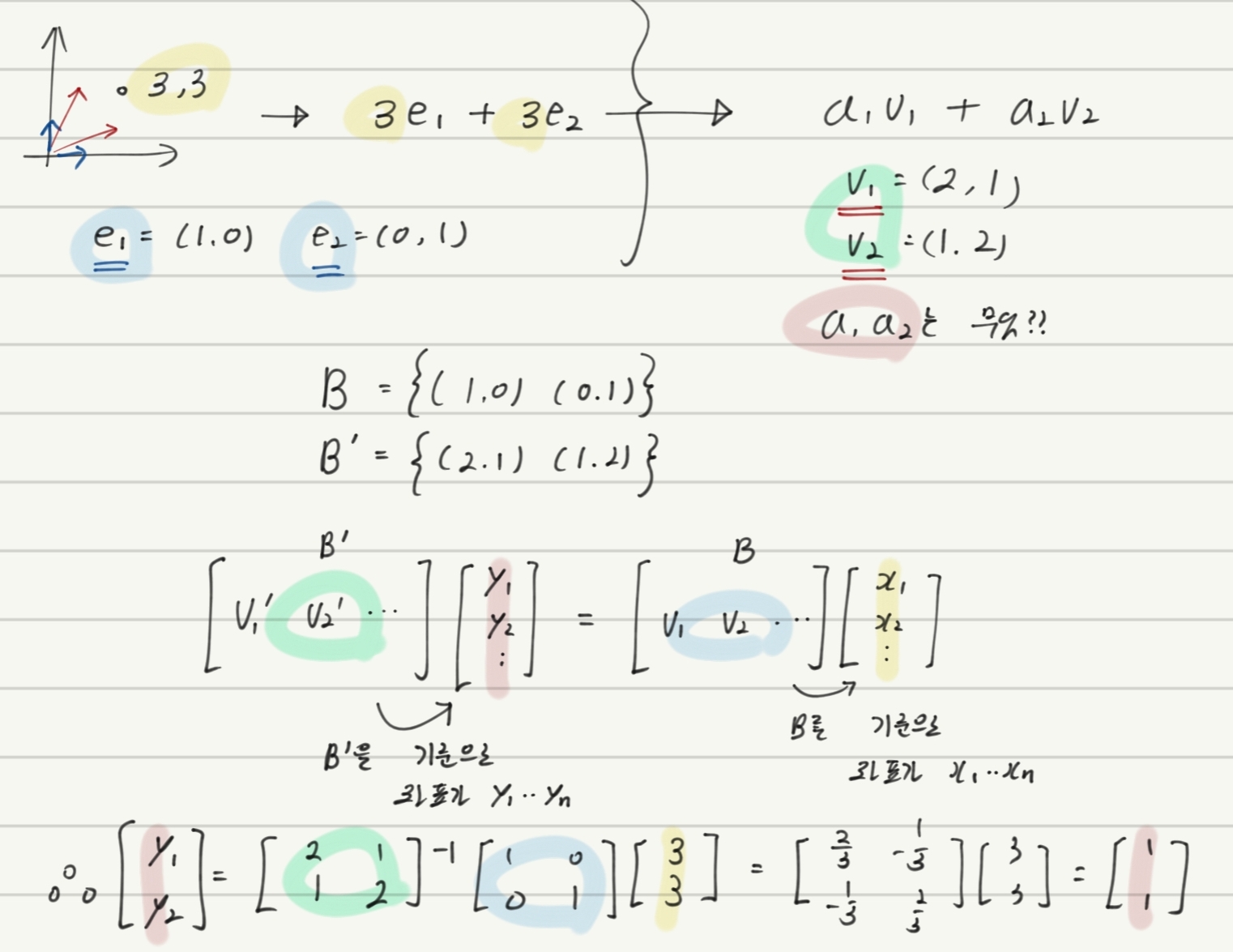
- 해석 : B를 기저로 하는 좌표값이 x1~xn 이라면, 그 좌표를 B’을 기저로하는 좌표값으로 바꾸면 어떤 좌표 y1~yn이 되는가? 에 대한 공식이다.
- 예제 :
- (2,1)E는 E의 백터들에 2와 1의 계수로 선형결합 해준 백터 = v1 을 의미함.
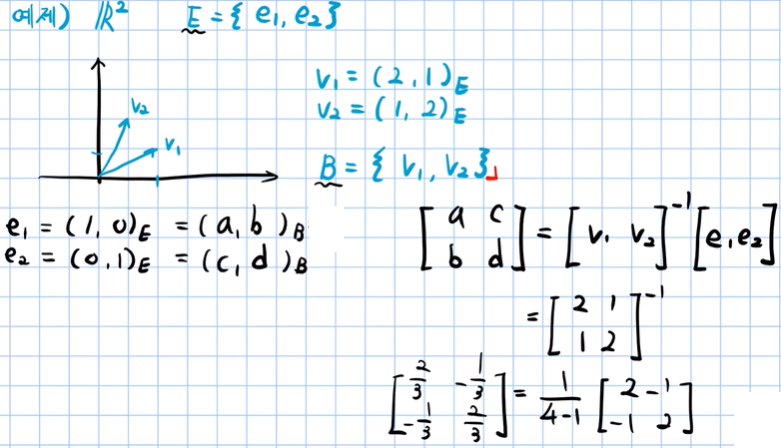
- E = {e1,e2,e3 … en} -> V = {v1,v2,v3 … vn} | e1과 v1은 백터 | v끼리는 서로 정규일 필요는 없다.
- 48강 기저변환과 대각화(= EVD(Eigen Value Decomposition) 기초)
- 대각화 : P * A * inverse(P) = D’(대각행렬) -> A =inverse(P) * D’(대각행렬) * P
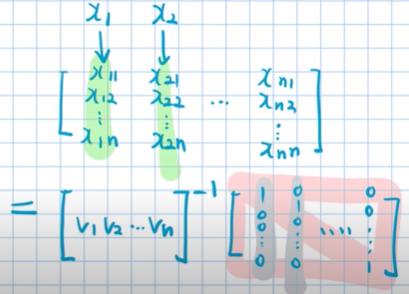
- 위의 일반화 공식과 고유백터&고유값을 이용해 대각화 공식을 찾아보자.
- 대각변환 : 축을 기준으로 상수배(확대/축소)하는 변환
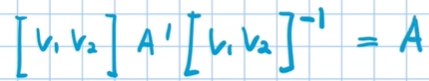 에 대해서 자세히 알아보자. 동영상에서는 위의 기저변환 일반화 공식을 이용해서 아래의 대각화 공식을 정의하고 있다.
에 대해서 자세히 알아보자. 동영상에서는 위의 기저변환 일반화 공식을 이용해서 아래의 대각화 공식을 정의하고 있다.- [v1 v2] A’ [v1 v2]-1 = A’ 을 A의 고유백터 좌표를 기준으로 기저변환한 ‘결과’
- [v1 v2] A’ [v1 v2]-1 = 위 ‘결과’를 다시 E를 기준으로 기저변환한 결과 = A !!
- A와 A’은 위의 x1~xn, y1~yn과 같은 역할이다.
- A’ 은 A의 고유값들로 만든 대각행렬, [v1 v2]는 A의 고유백터를 열백터로 가지는 행렬
- A 는 [E(기본 좌표계)]를 기준좌표계(기저)로 생각하는 선형변환이다.
- 고민을 많이 해야하므로 위의 내용을 이해하고 싶으면 강의를 다시 보자.
- 이 대각화 공식을 다음과 같이 증명하면 쉽게 이해 가능하다.
- 49강 대각화가능행렬과 그 성질들

- 대각화 가능한 행렬 A는 n개의 선형독립인 고유백터를 가진다.
- n개의 선형독립인 고유백터를 가지는 A는 대각화가 가능하다.
- 대각화 왜해??
- 대각행렬(D)은 n승을 하면, 대각원소의 n승인 행렬이다.
- A^n = P * D^n * inverse(P)
- A^n을 대각화로 엄청 쉽게 구할 수 있다!!
- 50강 - 증명 : n차원에서 ‘n개의 원소를 가지는 백터 v’들의 선형독립 백터(v1 v2 … vn)의 최대갯수는 n개이다.
- 51강 - 증명 : (1) A의 span(열백터들 or 행백터들) = n이면, A는 가역행렬이다. (2) 가역행렬(n차 정사각행렬)의 행백터, 열백터는 n dimention의 기저백터(독립!, 정규일 필요 X)이다.
Matrix similarity, Fuctnion, Space(닮음과 함수, 공간)
- 52강 Matrix similarity(행렬의 닮음)
- 두 행렬이 서로 닮음이면, 아래와 같은 많은 성질을 가진다.

- 53강 kernal and range(핵과 치역)
- kernal : (m x n 행렬 (n차원 백터 -> m차원 백터 로 변환하는 행렬)) 선형사상 F행렬 (=선형함수,=선형변환)에 대해, F * x = {0백터}. 즉 F에 의해서 0백터가 돼버리는 백터(n차원 공간의 좌표)들. 이 백터들을 kernal, null space(영공간) 이라고 한다.
- 선형사상 F에 의해서 n차원의 부분공간(원소들을 스칼라배, 덧셈을 하면 ‘집합 내의 원소’가 나오는 공간)이 m차원의 부분공간으로 변환됨
- 선형변환 행렬 A에 대해, range(A) (Ax의 공간. x는 백터) = col(A) (A의 colum space 차원)이다.
- 더 이해하고 싶으면, 53강 보충강의 보기
- 54강 일대일 합수
- 집합의 갯수를 새보자. A = {1,3,4} 3개이다. 새로은 집합 B의 갯수는 몇게 일까?
- 집합 A와 B의 원소의 갯수가 같으려면, A와 B사이의 일대일 대응 함수가 존재함을 증명하면 된다.
- 따라서 자연수집합과 정수 집합은 원소의 갯수가 같다. (일대일대응함수는 동영상 참조)
- Thm : T ( R^n -> R^m ) 이라는 선형사상 T에 대해서, ‘T가 일대응 함수이다.’와 ‘kernal(T) = {0}이다.’ 는 동치이다.
- 증명은 동영상 참조
- 집합의 갯수를 새보자. A = {1,3,4} 3개이다. 새로은 집합 B의 갯수는 몇게 일까?
- 55강 전사 함수
- 단사 : 일대일 대응이고 치역에 남은 원소가 있어도 됨.
- 전사 : 일대잉 대응이고 치역에 남은 원소가 없다. 모든 정의역에 치역에 대응 됨.
- 추가 증명 및 내용은 동영상 참조
- 56강 직교여공간
- 영공간(null space)
- 행공간 = 영공간
- rank (행백터 중 기저가 될 수 있는 백터의 최대 갯수)
- 직교여공간(orthogonal complement)
- 추후에 배울 최소제곱법에서 필요한 내용이다.

- non empty set : 영공간이 아닌 백터 집합
- V = (1,1,1)의 직교여공간은 (1,1,1)를 법선백터로 가지는 평면이다.
- 직교여공간에 0백터는 무조건 들어가 있다. 어떤 백터든 0백터를 곱하면 0백터가 되므로.
- 57강 행공간의 보존
- …
- 74강까지 패스. 너무 수학적임 나한테 아직 필요 없음.
Orthogonal Diagnalizing & Eigen Value Decomposition & SVD
- 75강 대각화가능 행렬(EVD, 교유값 분해)
- 대각화 가능한 행렬은 n개의 선형독립인(정규일 필요 X) 고유백터를 가진다. = 모든 열백터가 독립이다. = 가역행렬이다.
- 77강 직교행렬
- A 직교행렬 : A의 모든 열백터(and 행백터)는 서로 orthonormal(정규) 하다.
- 직교 변환 : 두 백터 v1,v2에 대해서 선형변환을 해도 두 백터의 길이(norm)이 유지되고, 두 백터와의 각도도 변하지 않는 변환을 말한다.
- 78강 직교행렬의 조건
- (참조 transpose(T), trace(대각합) 서로 헷갈리지 말자.)
- inverse(A) = transpose(A)이면 A는 직교행렬이다.
- A가 직교행렬이면 A의 행백터는 모두 orthonormal 하다.
- A가 직교행렬이면 transpose(A)도 직교행렬이다.
- 이 모든것의 증명은 동영상 참조. 하지만 직교변환의 개념을 사용하므로 쉽지 않다. 일단 다 외어.
- 79강 켤레 전치와 대칭 함수
- 켤레 전치(confugate transpose) : A가 복소행렬(원소가 복소수)일 때, A의 결레전치행렬은

- 을 말한다. bar(A) : 모든 원소에 켤레복소수화. (1+i -> 1-i)
- 컬레 전치의 기본 성질
- (A*)* = A
- (AB)* = (B*A*)*
- 원소가 모두 실수로 이뤄진 ‘대칭행렬’의 고유값은 항상 실수 이다.
- 증명은 동영상 참조.
- 켤레 전치(confugate transpose) : A가 복소행렬(원소가 복소수)일 때, A의 결레전치행렬은
- 80강 직교대각화 가능(Orthogonal Diagonalizability)
- 직교 닮음 이란?
- C = inverse(P) * A * P (이때 P는 직교 행렬 : inverse(P) = transpose(P))
- C는 A와 닮음이고, A는 C와 닮음이다.
- 아래는 C가 D (대각행렬)
- 직교 대각화(orthogonal diagonalizability)
- 직교 닮음 이란?
- 81강 orthogonal diagonalizing (직교 대각화 하기)=Eigen Value Decomposition 시작
- 대칭행렬이면 직교대각화가능 행렬이다.
- 대칭행렬을 직교대각화 하는 방법.
- A가 대칭행렬이면, A의 고유백터들은 서로 ‘독립’일 뿐만 아니라 ‘직교’한다. = (‘서로 다른 고유공간’에 속한 고유백터는 서로 직교한다.)
- ‘서로 다른 고유공간’ 이란?
- 하나의 고유값에 대해서, 여러개의 고유백터들(1) 존재 가능(ex. 상수배 등)
- 다른 고유값에 대한, 고유백터들(2)이 존재 할 때.
- 고유백터들(1)과 고유백터(2)는 서로 직교한다. (당연한 얘기지만 일단 참고)
- (아래) 선형변환 A를 내적 안에다 넣을 때는 inverse(A)가 들어간다. 증명은 17강 or 75강 참조.

- ‘서로 다른 고유공간’ 이란?
- 직교대각화하는방법
- A는 대칭행렬이다.
- A의 n개의 고유값을 구한다.(실수 고유값이 나온다.)
- 고유값에 맞는 orthonormal basis(단위 고유 직교 백터) n개 백터들을 구한다.
- 위의 n개의 백터를, 열백터로 가는 행렬 P를 만든다.
- inverse(P) A P = D(고유값으로 만든 대각행렬)
- 즉 A가 P에 의해서 대각행렬이 되었다.
- 직교대각화 예제
-

- 그람슈미트 변환을 알면, 고유값의 중근이 존재할 때, 중근인 고유값에 대한 2개의 기저백터를 뽑아내는 방법을 알 수 있다.
-
- A가 대칭행렬이면, A의 고유백터들은 서로 ‘독립’일 뿐만 아니라 ‘직교’한다. = (‘서로 다른 고유공간’에 속한 고유백터는 서로 직교한다.)
- 82강 고유값 분해를 이용한 이미지 손실 압축(Eigen Value Decomposition)
- 83강 SVD(Singular Value Decompostion)
- 바로 위의 Eigen Value Decompostion의 시작은 대칭행렬이다! 대칭행렬만, 직교 대각화가 가능하므로.
- A가 대칭행렬이 아니고, 정사각행렬이라면?? ㅠㅠ 직교대각화 (P * D * transpose(P)) 불가능!
- A = U * Σ * transpose(V) 로 분해해보자.
- A * transpose(A)는 대칭행렬이기 때문에, 교유백터들은 모두 독립일 뿐만 아니라 직교하다. 이 고유백터들을 각각 정규화(norm = 1)로 만들어 준 행렬이 아래의 V이다.

- 84강 SVD 예제
- 85강 특이값 분해 일반화 (정사각행렬이 아닌 A)
- 86강 축소된 특이값 분해