【LinearAlgebra】선형대수 정리 2 (한글강의)

in Self Study

쑤튜브 선형대수 강의내용 정리 24강~44강

youtube 강의 링크 : 쓔튜브 선형대수 강의 링크

선형 결합과 선형독립

  • 24강 선형결합(Linear combination)과 생성(Span)
    • 데카르트 좌표계(2차원 직교 좌표계) : 하지만, 좌표계는 꼭 직교(직각)이어야만 하는 것은 아니다. 평행이 아닌 두 직선으로 좌표계를 표현할 수도 있다.
    • 3차원 이상의 좌표계를 표한하려고 할때, 주어진 백터 n개가 n차원 좌표계의 좌표축이 될 수 있는지 없는지를 판단하는 것이, 선형독립 판단이다.
    • Linear combination (선형 결합) : v1,v2,v3의 각각의 스칼라곱의 합에 의해서 v를 표현할 수 있다면, v를 v1,v2,v3의 선형결합이다. 라고 한다. Ex) v = a*v1+ b*v2 + c*v3
    • Span(v1, v2, v3, v4, v5 … )이란 v1, v2, v3, v4, v5 …이 만들 수 n차원 공간을 말한다. 백터들이 서로 독립이면 n공간 그대로 가진다. 하지만 종속이면 n미만의 공간이다.
  • 25강 선형독립(linearly independent)
    • 선형 독립의 정의
    • image-20201120172426393
    • 영백터는 모든 백터들과 독립이 아니다. (위의 정의에 그대로 대입해서 생각해보기)
    • 선형독립의 집합은 공집합을 제외한 모든 부분집합은 선형독립 집합이다.
    • 3차원 열백터 4개에 대해서, 3x4행렬의 확장행렬을 만들고, 왼쪽 3x3 블락에 대해서 기약행사다리꼴 모양으로 만들어준다.(기양행사다리꼴로 구하는 해는 c1, c2, c3이다.) 이때 왼쪽 3x1의 값이 0이 아니라면 선형종속이다. (consisitent) 반대로 왼쪽 3x1의 값이 0이라면 선형독립이다.
    • n차원 열백터 n개를 묶은 n x n 행렬의 역행렬이 존재한다 = 그 행렬의 기약행사다리꼴 단위행렬 이다. = n차원 열백터 n개는 서로 독립니다.
    • 선형 독립 판별법 : 동차 연립 선형 방정식(이전 강의 참조)이 자명해만을 가지면, 독립이다. 즉! 열백터로 만든 행렬이 가역행렬이면, 그 열 백터들은 독립이다.
    • 그 열백터 n개로 n차원 좌표계를 표현할 수 있다. Span(v1, v2, v3, v4, …vn ) = R^(n) 이다.
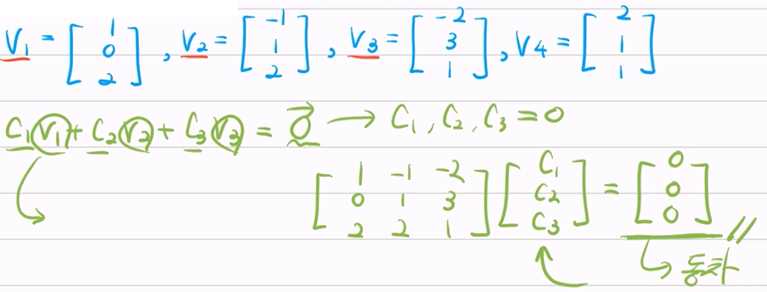
    • image-20201120173335391
  • 26강, 27강 해집합의 성질
    • column space, row space : 행렬을 열 백터, 행 백터의 관점으로 봤을 때, 만들수 이는 span(A) 차원의 공간
    • A의 열백터가 선형독립이면 A는 가역행렬이다. 그렇다면, transe(A)의 행백터가 선형독립이다. A가 가역행렬이면 transe(A)도 가역행렬이다. 따라서 B의 행백터가 선형독립이면, B는 가역행렬이다.
    • 행렬 A의 열백터가 선형독립이면, 열백터의 일차 계수 선형결합으로 span(A)차원 백터 V가 있을 때, 그 일차 계수들(x1,x2,x3,x4…) 는 유일하다. AX = V -> X = inverse(A) x V 는 유일하므로.
    • AX = 0가 자명해 만을 가지면 A의 열백터는 선형독립니다. = transe(A)도 가역이다. A의 행백터도 선형독립이다.

LU decomposition

  • 29강 LU decomposition
    • AX = b에서 X를 구하는 방법은, 확장행렬 변환후 기약형사다리꼴로 바꾸는 방법이 있다. 하지만 다른 좋은 방법은 없을까?
    • 대각 행렬 : 대각선의 성분을 제외한 모든 부분이 0인 행렬. 대각행렬은 가역행렬이다. 대각행렬의 역행렬은 대각 성분을 모두 역수 취해준 행렬이다. 하지만 대각 성분 중 하나라도 0이 존재한다면 역수를 취하는 게 불가능하다. 따라서 대각행렬의 대각 성분 중 하나라도 0이 존재하면 비가역행렬이다.
    • 삼각행렬 : 대각성분을 기준으로 위(Lower) or 아래(Upper)가 모두 0인 행렬이다. 대각 행렬은 삼각행렬의 한 원소이다. 이 삼각행렬의 대각성분 중 0이 존재하지 않는다면, 가오스조던 소거법에 의해서 (forward, backward 둘 중 하나만 해서) 기약형사다리꼴로 바꿀 수 있다. 즉 가역행렬이다.
    • A = LxU (Lower triangular matrix) x (Upper triangular matrix)
    • image-20210106160928953
  • 30강, 31강 LU분해의 이론적인 근거와 계산법
    • 가우스 소거법(forward)을 시행할 때 사용되는 모든 기본행렬은 항상 Lower triangular matrix(하삼각행렬)이다. (행교환 제외. 행교환 기본행렬은 하삼각행렬이 아니다.)
    • 하삼각행렬꼴의 기본행렬의 역행렬은 하삼각행렬이다.
      • image-20210106161532372
    • 하삼각행렬 x 하삼각행렬 = 하삼각행렬 이다.
    • 위의 3가지 이론을 근거로 아래와 같이 표현할 수 있다 . 여기서 A에 대한 가오스 소거법(forward)과정은 Ek… E2 E1 (기본행렬 곱)이라고 표현할 수 있다.
      • image-20210106162215984
    • 따라서 LU를 구하는 방법은 아래와 같다.
      1. A에 대한 [가오스 소거법을 모아놓은 기본행렬들(행교환 제외)]을 찾는다.
      2. (그 기본행렬들의 곱) x A = U이다. U를 구했다.
      3. inverse(그 기본행렬들의 곱) = L이다. L을 구했다.
    • 하지만! LU분해를 해서 나오는 L,U는 유일하지 않다. 여러개가 나올 수 있다.
  • 32강 PLU분해
    • A에 대한 [가오스 소거법을 모아놓은 기본행렬들]을 찾을 때 행교환이 꼭 필요하다면 어떡하지??
    • 그렇다면! A에서 필요한 [행교환 기본행렬들(!= 하삼각행렬)]을 모두 찾아놓고, 그것들의 곱을 P라고 하면 된다.

Determinant (33강~39강)

  • 33강 행렬식,판별식
    • 2차 행렬의 판별식 공식을 구하는 방법
    • 3차 행렬의 판별식 공식을 구하는 방법(크래머의 공식) -> 동영상 참조
    • 4차 행렬의 판별식 공식을 구하는 방법
  • 특수한 경우의 determinant
    • 대각행렬, 삼각행렬의 determinant = 대각원소의 곱이다.
    • 영행, 영열을 포함하는 행렬의 determinant는 0이다.
  • 나머지 강의는 나중에 필요하면 보자.

Eigen value & Eigen vector

  • 40강 고유값과 고유벡터
    • 관점(좌표축)을 달리해서 보이지 않던 것을 찾아보자.
    • Ax = λx 이때, λ = Eigen value, x = Eigen vector A = invertible
    • n개의 고유백터는 서로 독립이다. 그리고! n개의 고유백터는 서로 orthogonal (백터의 내적은 0)하다.
  • 41강, 42강 특성방정식 (Characteristic Equation)
    • Ax = λx -> (A-λI)x = 0, 이때 det(λI-A) = |(λI-A)|를 특성 방정식이라고 한다.
    • 그리고 이 특성방정식의 해(λ)들이 고유값들(λ)이다.
    • (A가 n차 정사각행렬일때) 특성방정식의 해가 n개 이면, 선형독립인 고유백터 n개를 찾아낼 수 있다. (증명은 동영상 참조 굳이 알 필요 없음)
  • 43강, 44강 특수한 행렬들의 고유값
    • 대각행렬 : 대각원소가 결국 고유값이다.
    • 삼각행렬 : 대각원소가 결국 고유값이다.
    • nxn 행렬 A의 고유값을 λ1, λ2, λ3 — λn 이라 하면, 아래와 같이 정의할 수 있다. (증명은 43강44강 참조)
      • det(A) = λ1 x λ2 x λ3 x — x λn
      • trace(A) 대각합 = λ1 + λ2 + λ3 + — + λn

© All rights reserved By Junha Song.