【LightWeight】Understanding DenseNet, MobileNet V3 from youtube w/ advice
- 논문1 : MobileNet V3 / Youtube Link1
- 논문2 : DenseNet / Youtube Link2
- 분류 : Light Weight
- 공부 배경 : MobileNetV3 Paper 읽기 전 선행 공부로 youtube 발표 자료 보기
- 선배님 조언:
- 삶의 벨런스? 석사 때는 그런거 없다. 주말? 무조건 나와야지. “가끔은 나도 쉬어야 돼. 그래야 효율도 올라가고…” 라고 생각하니까 쉬고 싶어지는 거다. 그렇게 하면, 아무것도 없이 후회하면서… 석사 졸업한다. “딱 2년만 죽었다고 생각하고 공부하자! 후회없도록! 논문도 1학년 여름방학 안에 하나 써보자!”
- 평일에는 1일 1페이퍼 정말 힘들다. 평일에는 개인 연구 시간 하루에 1시간도 찾기 힘들다. 그나마 주말에라도 해야한다. 지금이야 논문 읽고 배운 것을 정리하는게 전부지만, (1) 학교 수업 듣기 (2) 논문 읽기 (3) 코딩 공부 하기 (4) 코드 직접 수정하고 돌려보기 (5) 논문 쓰기. 까지 모두 모두 하려면 끝도 없다.
- 이번 여름방학 이전에, 아이디어 내고 코드 수정해서 결과 내보고 빠르게 제출하든 안하든 논문 한편 써보자.
- 1학기 초에 연구 주제 확정하자.
- 목차
- 강의 필기 PDF는 “OneDrive\21.겨울방학\RCV_lab\논문읽기”
- <아래 이미지가 안보이면 이미지가 로딩중 입니다>
1. Linear Bottlenecks Code
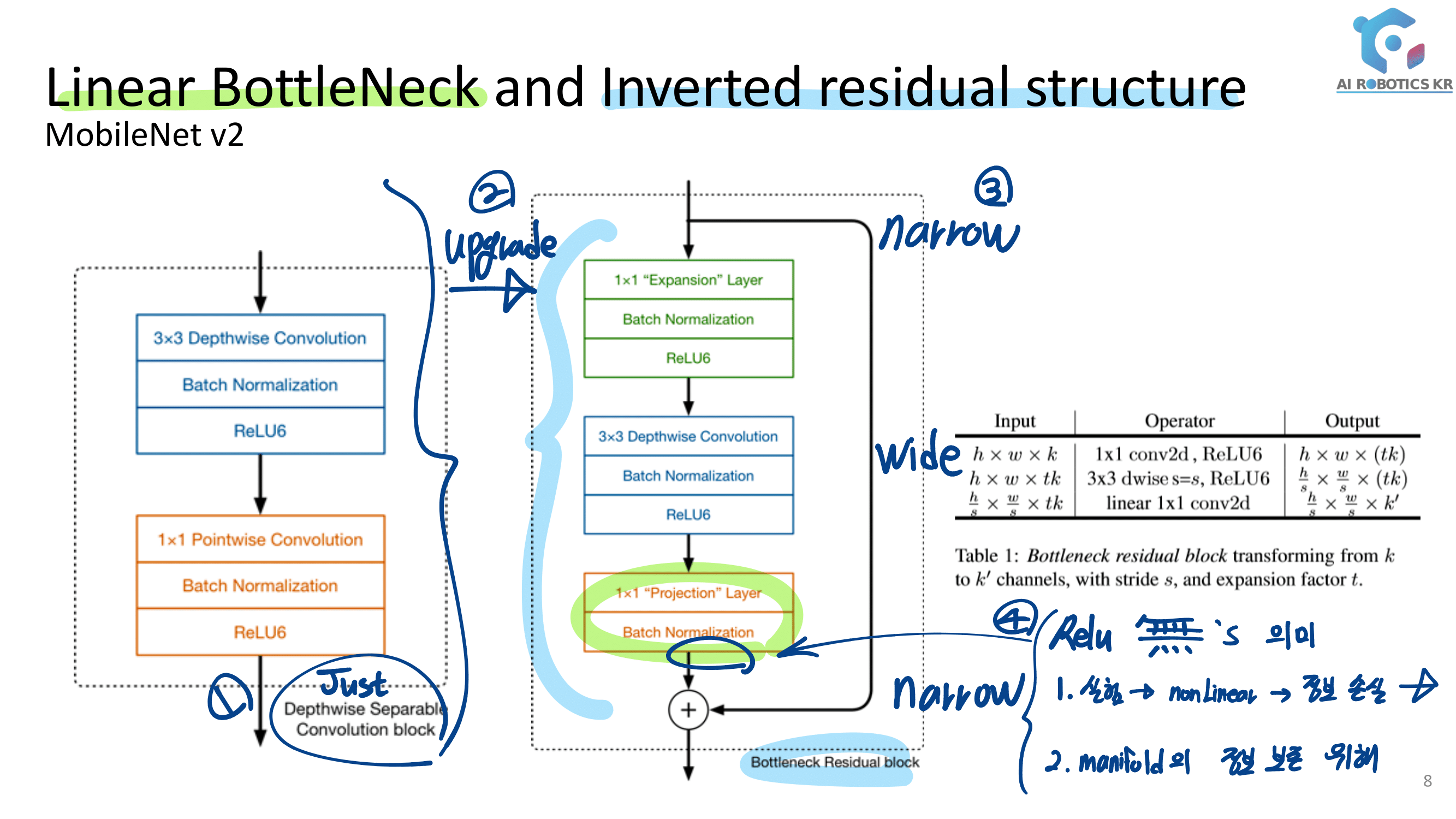
결국 Relu안하는 Convolution Layer이다. ㅅ… 욕이 나온네. “별것도 아닌거 말만 삐까번쩍하게 한다. 이게 정말 수학적으로 증명을 해서 뭘 알고 논문에서 어렵게 설명하는건지?, 혹은 그냥 그럴 것 같아서 실험을 몇번 해보니까 이게 성능이 좋아서 멋진 말로 끼워맞춘건지 모르겠다.
MobileNet V2 코드 - 파일이 1개 뿐이고 생각보다 엄청 쉽다. 이건 뭐 FPN 파일 하나 코드보다 훨씬 이해하기 쉽다.
class InvertedResidual(nn.Module): def __init__(self, inp, oup, stride, expand_ratio): super(InvertedResidual, self).__init__() self.stride = stride assert stride in [1, 2] hidden_dim = int(inp * expand_ratio) self.use_res_connect = self.stride == 1 and inp == oup if expand_ratio == 1: self.conv = nn.Sequential( # dw nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, groups=hidden_dim, bias=False), nn.BatchNorm2d(hidden_dim), nn.ReLU6(inplace=True), # pw-linear ***** 이거가 Linear Bottlenecks ***** nn.Conv2d(hidden_dim, oup, kernel_size=1, stride=1, padding=0, bias=False), nn.BatchNorm2d(oup), ) else: self.conv = nn.Sequential( # pw nn.Conv2d(inp, hidden_dim, 1, 1, 0, bias=False), nn.BatchNorm2d(hidden_dim), nn.ReLU6(inplace=True), # dw nn.Conv2d(hidden_dim, hidden_dim, 3, stride, 1, groups=hidden_dim, bias=False), nn.BatchNorm2d(hidden_dim), nn.ReLU6(inplace=True), # pw-linear ***** 이거가 Linear Bottlenecks ***** nn.Conv2d(hidden_dim, oup, kernel_size=1, stride=1, padding=0, bias=False), nn.BatchNorm2d(oup), )
- 매니폴드 학습이란, <그림 1>과 같은 형태로 수집된 정보로부터 <그림 2>와 같이 바르고 곧은 유클리디안 공간을 찾아내는 것을 말합니다.
- 아래의 그림처럼, 100차원 vector들이 100차원 공간상에 놓여있다. 하지만 유심히 보면, 결국 백터들은 2차원 평면(왼쪽 그림) 혹은 3차원 공간(오른쪼 그림) 으로 이동 시킬 수 있다. 즉 100차원 공간이라고 보여도 사실은 2차원 3차원으로 더 잘 표현할 수 있는 백터들 이었다는 것이다.
- 이렇게 높은 차원의 백터들을, 낮은 차원의 직관적이고 곧은 공간으로 이동시킬 수 있게 신경망과 신경망의 파라메터를 이용한다.

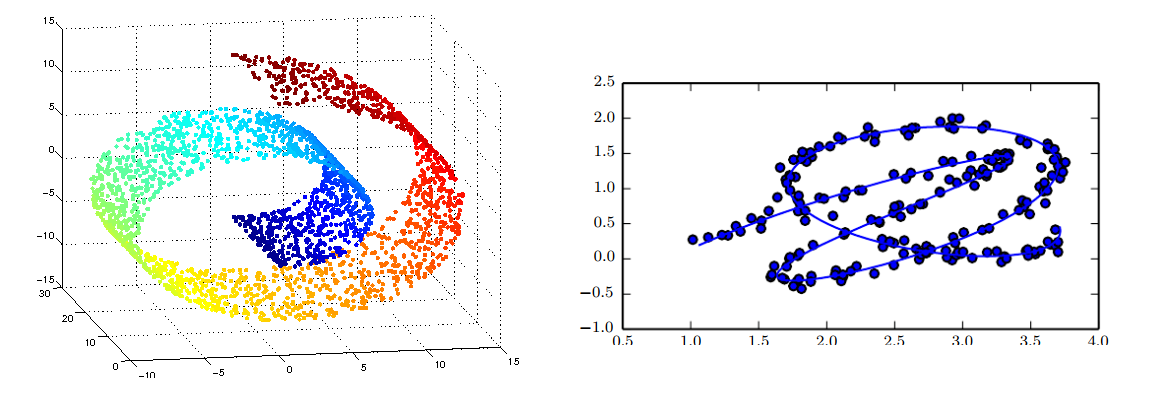
- 스위스롤(왼쪽그림)을 우리가 보면 3차원이지만, 그 위에 올라가 있는 개미가 느끼기엔 2차원이다.
- 매니폴드 학습이란 ‘눈을 감고(학습이되지 않은 상태에서) 비유클리디안 형태를 만져가며(데이터를 이용해) 모양을 이해해(모델을 학습해) 나가는 것이다’. 즉, 스위스롤을 2차원 평면으로 피는 과정이다.
- 오른쪽 그림과 같이 2차원 데이터를, 1차원으로 필 수 있다면 데이터와의 유사도 측정등에 매우 좋을 것이다.
- 혹은 차원을 늘리기도 한다. 예를 들어 오른쪽 그림의 실을 잡고 들어올리는 행위가, 차원을 늘리는 행위이고, 그것은 신경망의 Layer를 추가하는 행위라고도 할 수 있다.
Manifold of Interest 위의 내용까지 간략히 요약 정리!
- 실용적으로 말해서! “conv혹은 fc를 통과하고 activation function을 통과하고 나온 (Subset) Feature가 Manifold 이다!” 그리고 “그 Manifold 중에 우리가 관심있어하는 부분, 가장 많은 이미지의 정보를 representation하는 일부를 논문에서는 Manifold of interest 라고 한다.”

- 논문 설명 + 나의 이해 : Input data = x 가 맨 왼쪽과 같이 표현 된다고 하자. 그리고 Activation_Function( T * x) 를 수행한다. 여기서 T는 Input data의 차원을 위 사진의 숫자와 같이 2,3,5,15,30 차원으로 늘려주는 FC Layer라고 생각하자.
- 결과를 살펴보면, 낮은 차원으로 Enbeding하는 작업은, 특히 (비선형성 발생하게 만드는) Relu에 의해서 (low-dimensional subspace = 윗 이미지 그림을 살펴 보면) 정보의 손실이 많이 일어난다. 하지만 고차원으로의 Enbeding은 Relu에 의해서도 정보의 손실이 그리 많이 일어나지 않는다.
- 솔직히 논문이나 PPT내용이 무슨소리 하는지는 모르겠다.
- 결국에는 위와 같은 “정보 손실”을 줄이기 위해서, 비선형이 Relu를 쓰지 않고 Linear Function을 쓰겠다는 것이다.
<아래 이미지가 안보이면 이미지가 로딩중 입니다>
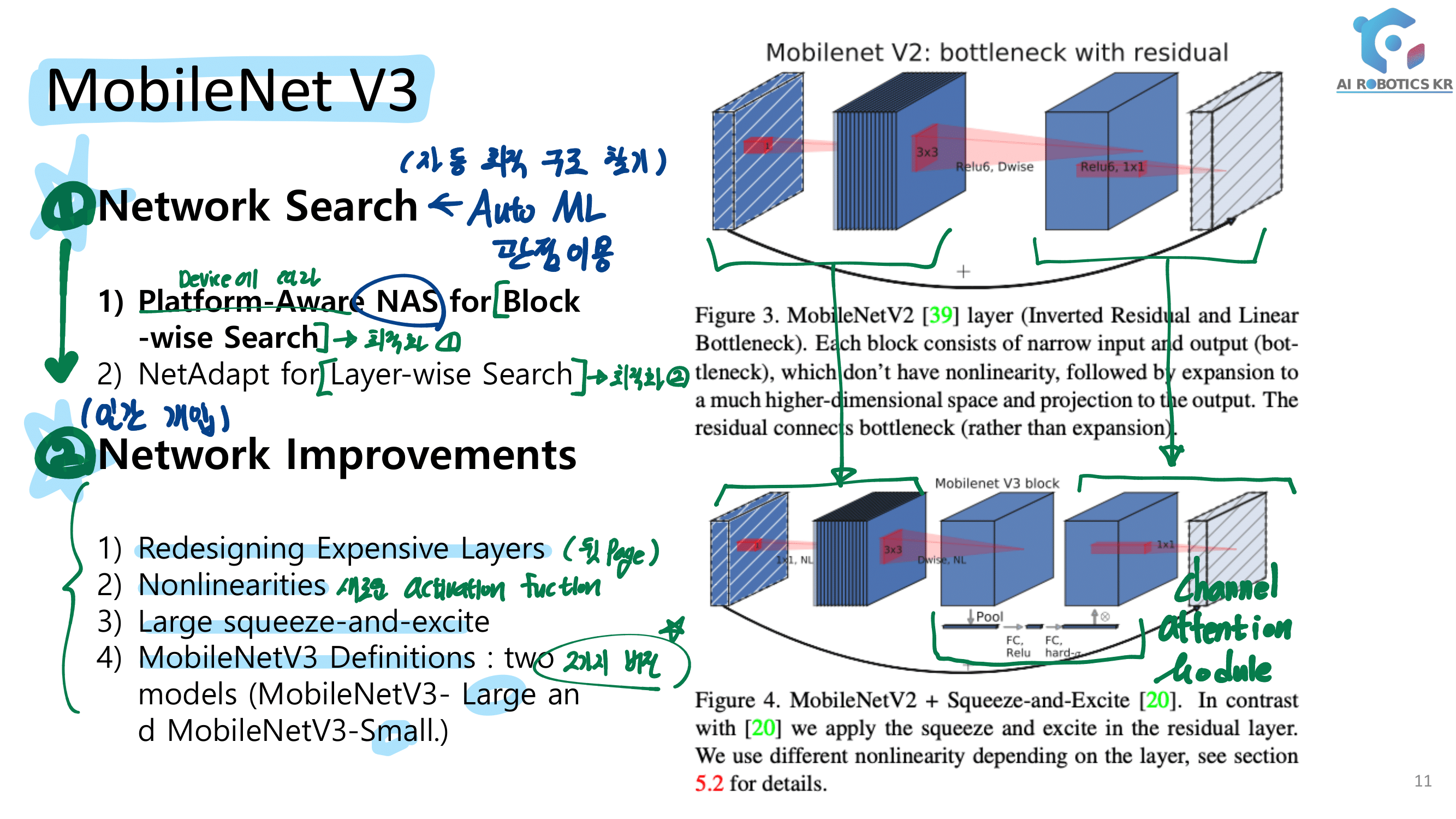
2. MobileNet V3
- 참고하면 좋은 블로그 (1). Blog1 (2). Blog2
- AutoML-and-Lightweight-Models
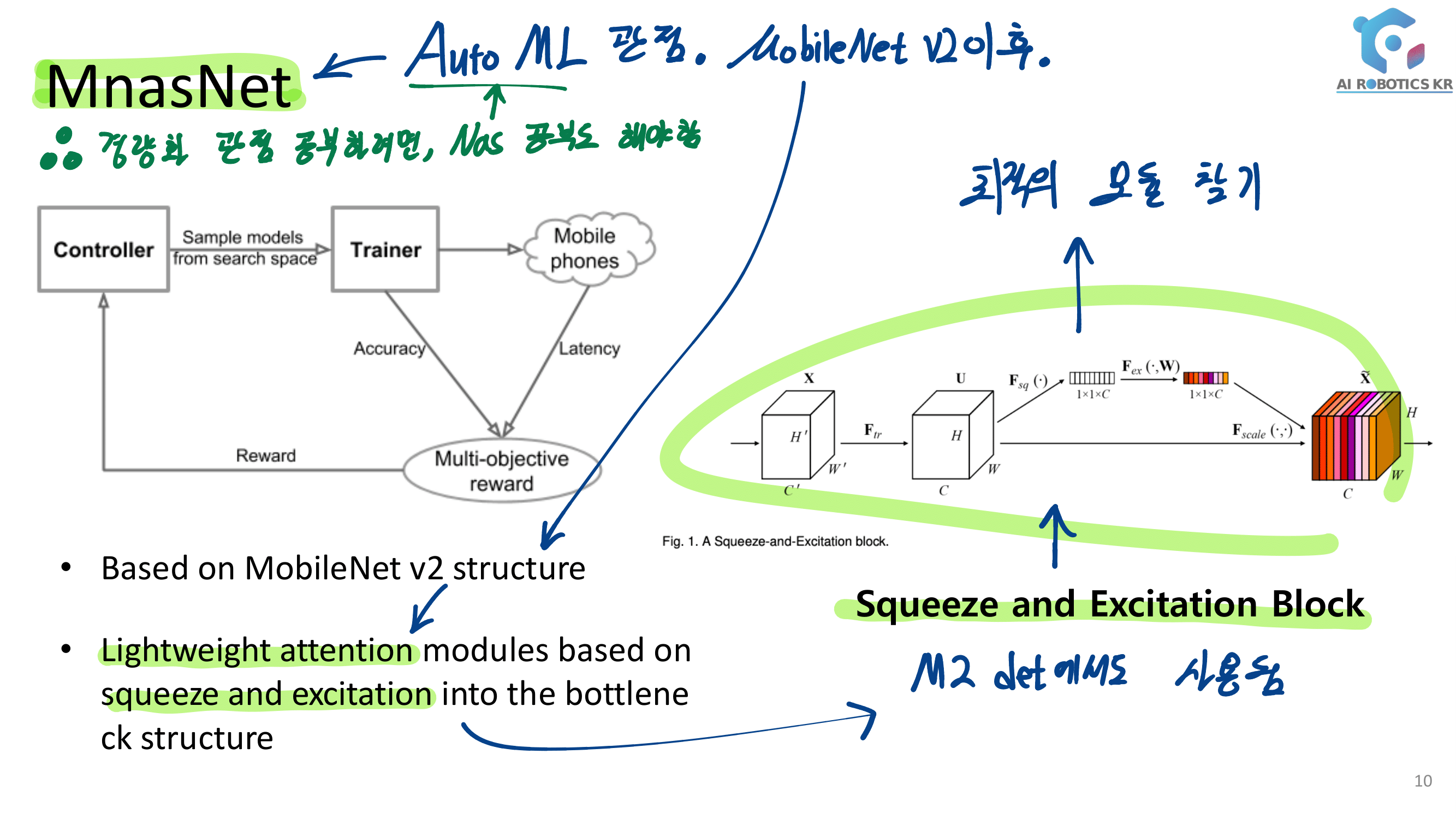
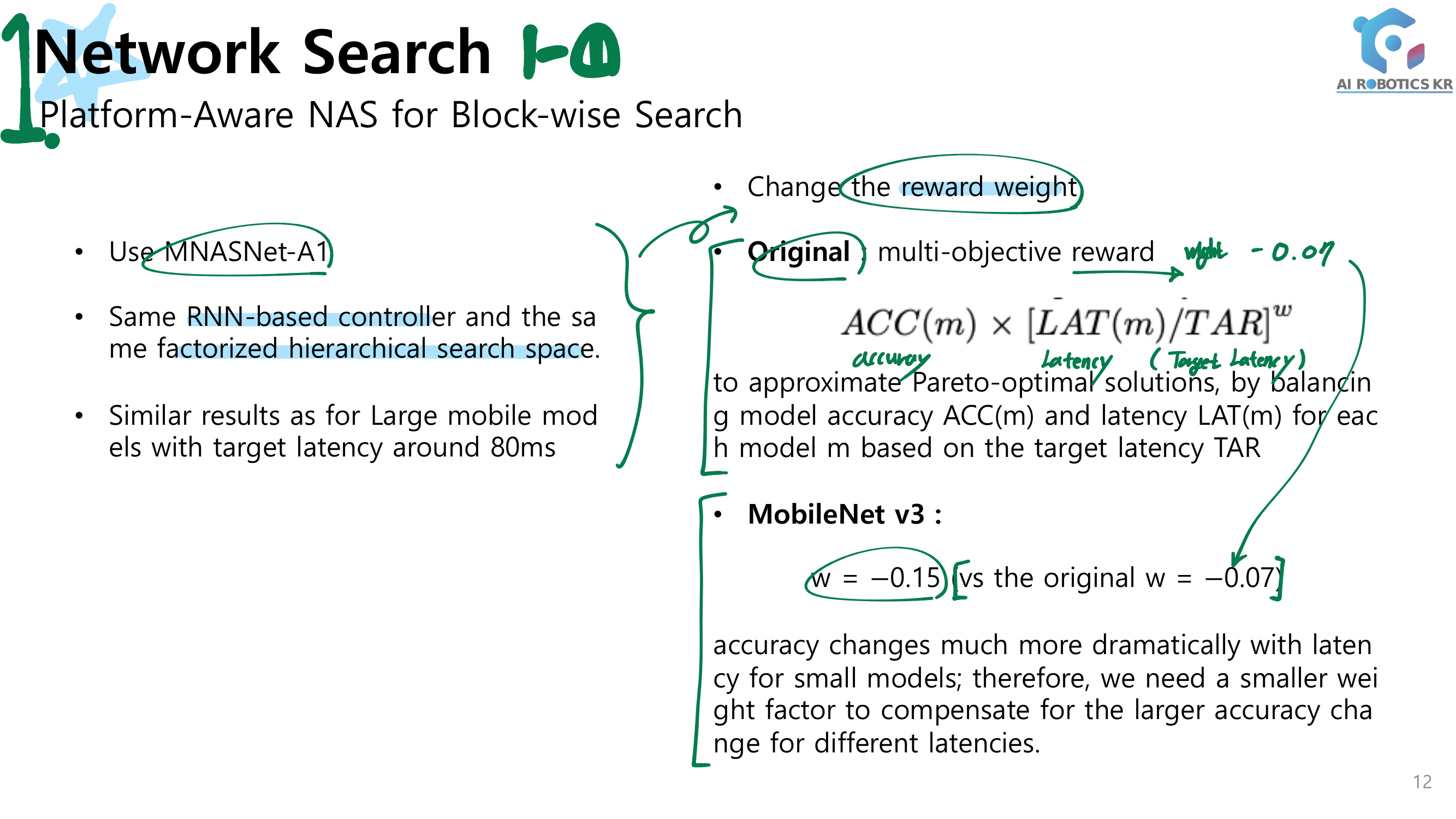
- 1.) Neural Architecture Search - Reinforcement 개념이 들어간다.
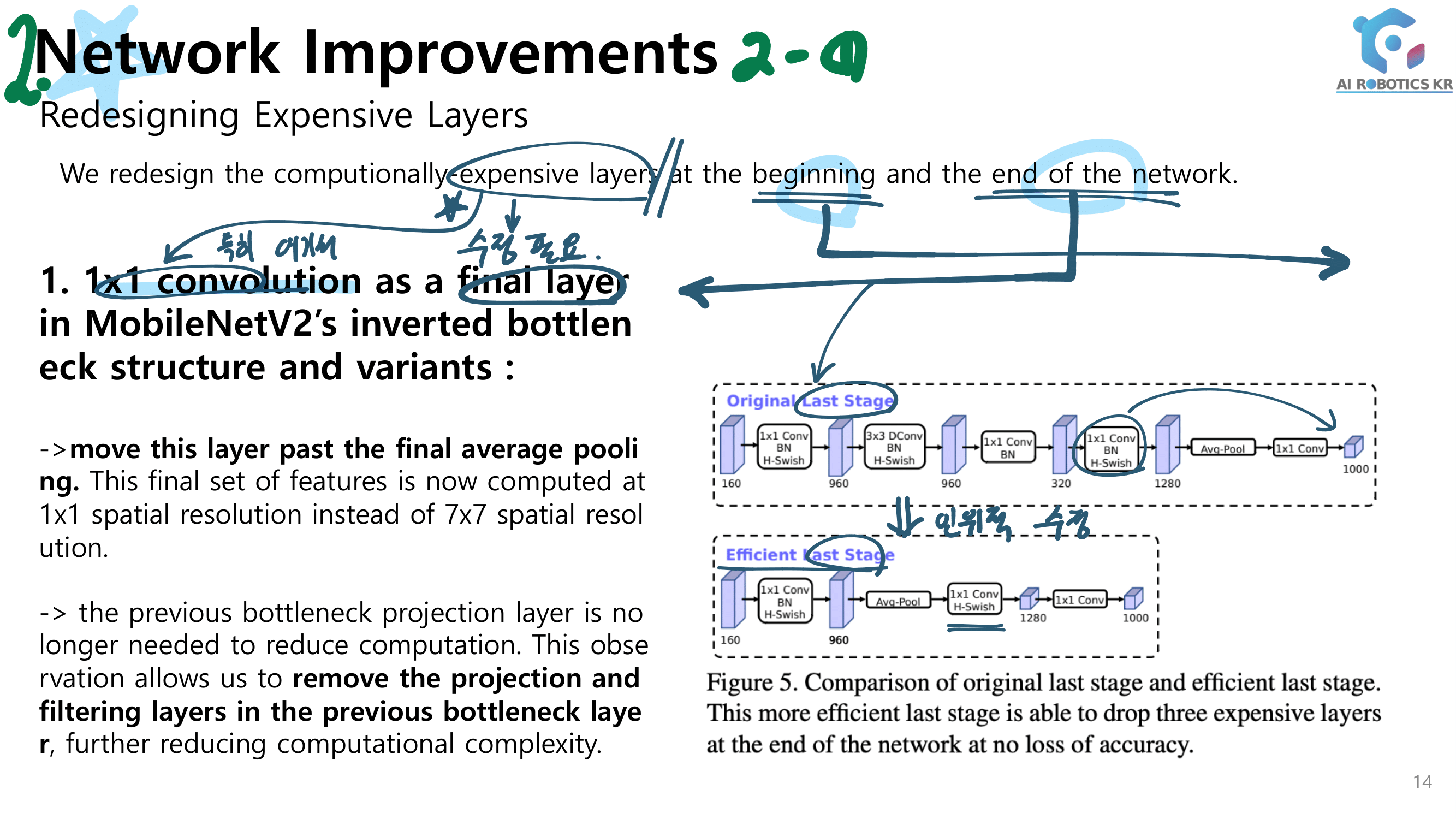
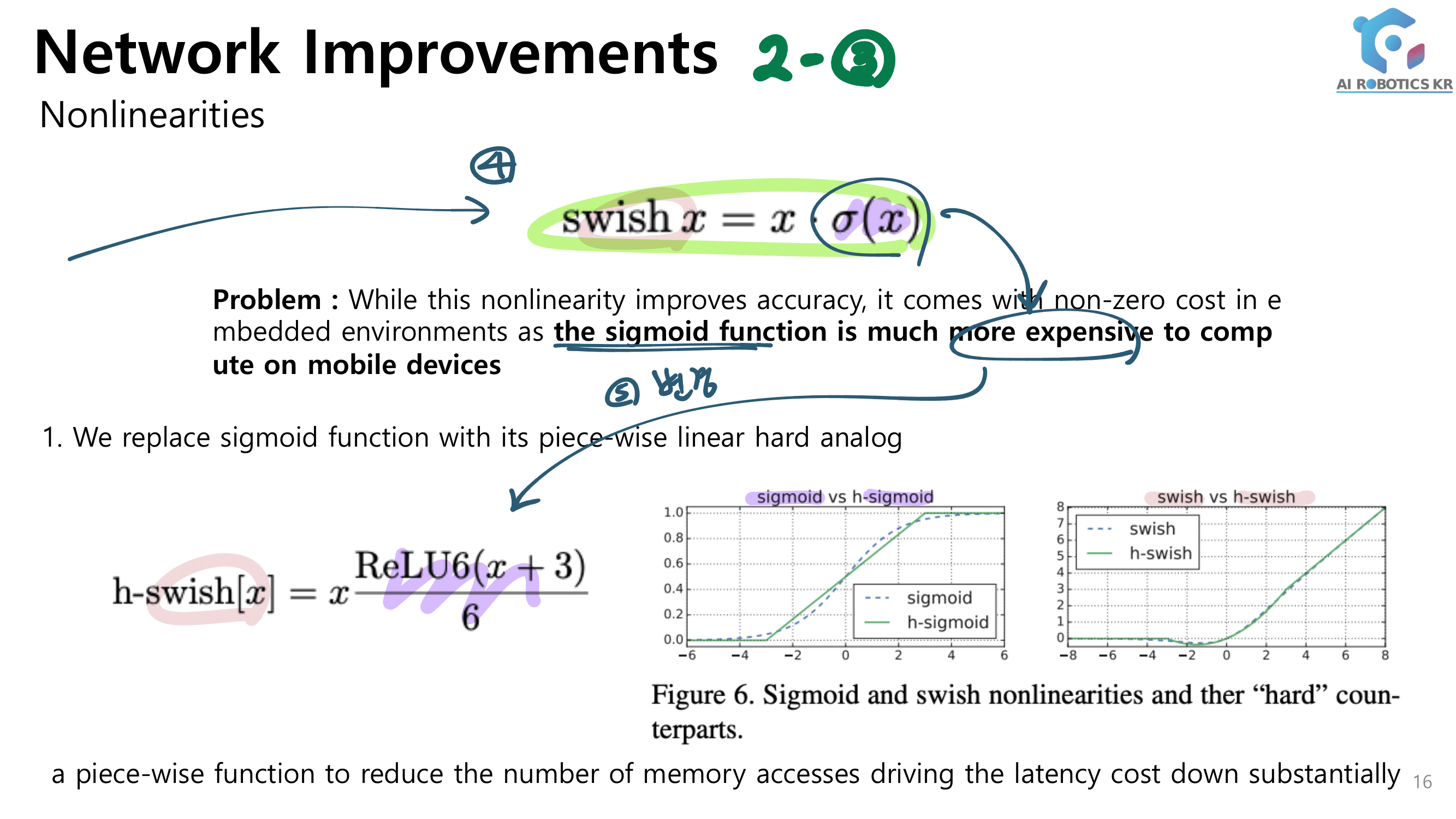
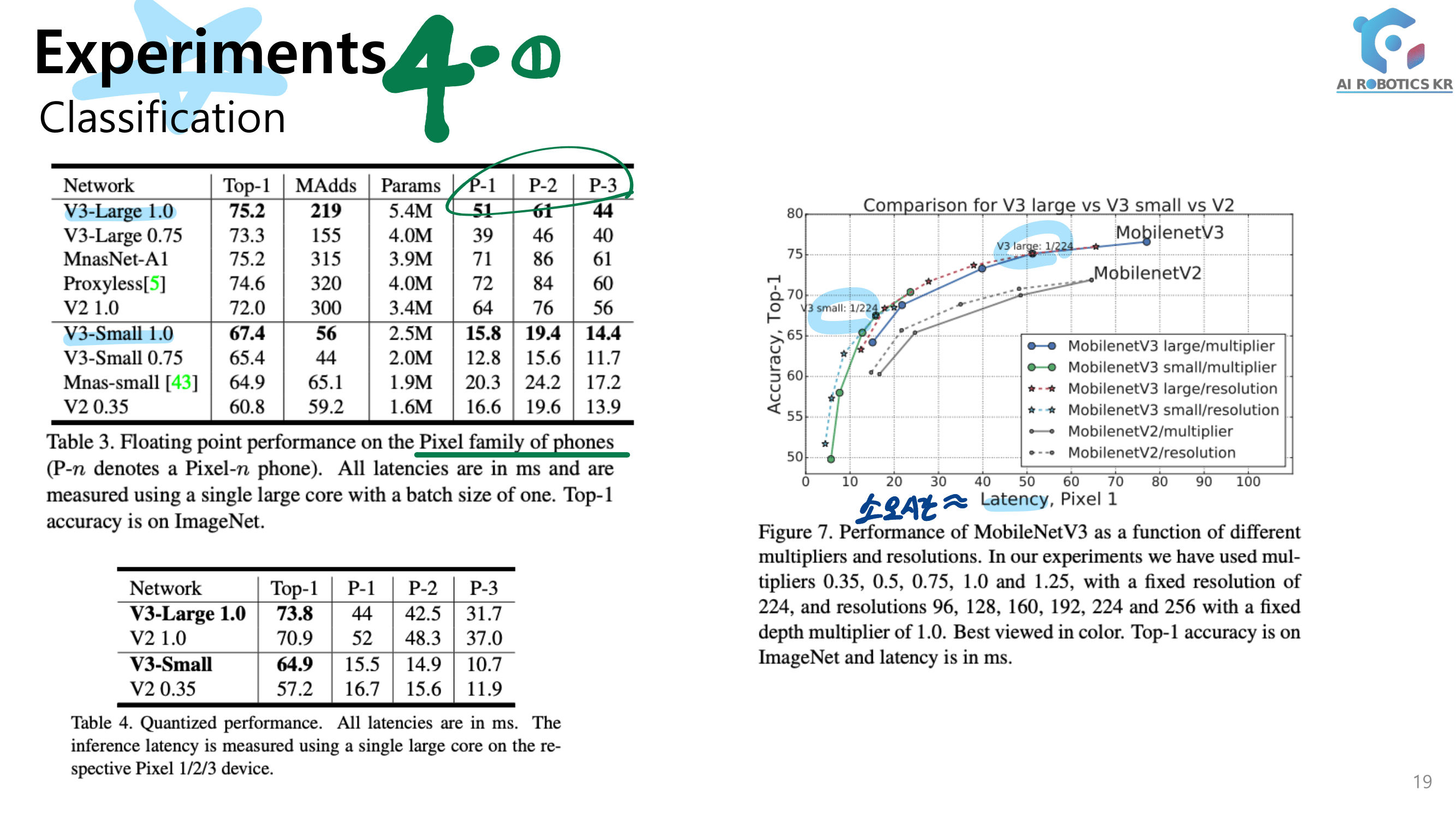
- 2.) Lightweight Structures
- 3.) Model Compression, Quantization and Acceleration
- 4.) Hyperparameter Optimization
- 5.) Automated Feature Engineering.
- 위의 개념이 많이 들어가기 시작해서 사실 들으면서, 거의 이해가 안됐다. 따라서 Lightweigh-Model 주제로 연구를 하게 된다면 그때 이해해야 겠다.
- 하지만.. 연구실 선배님들의 연구 주제와 비슷하게 가져가는게 낫기 때문에, 이 분야는 깊게 고민해보자.

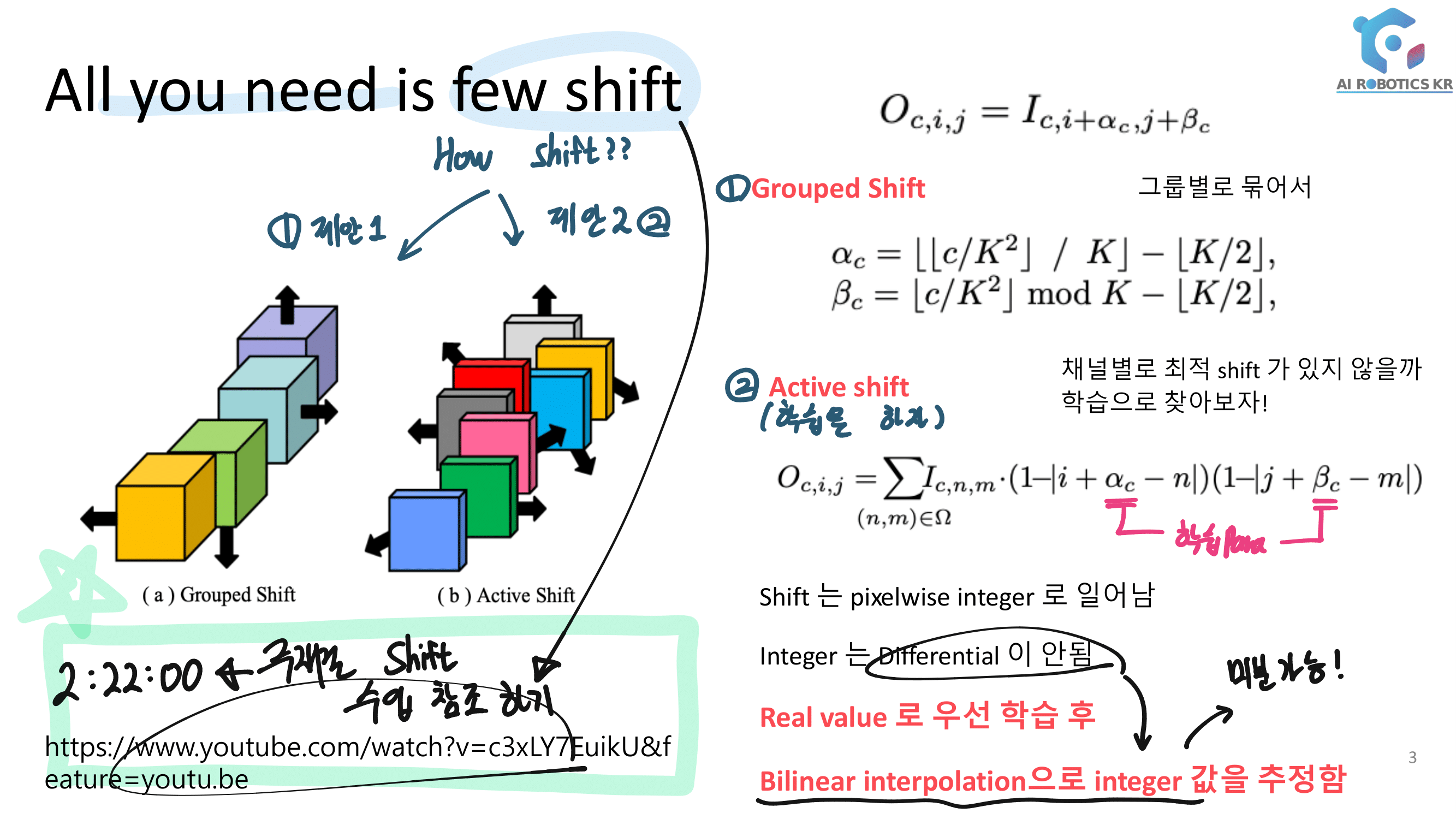
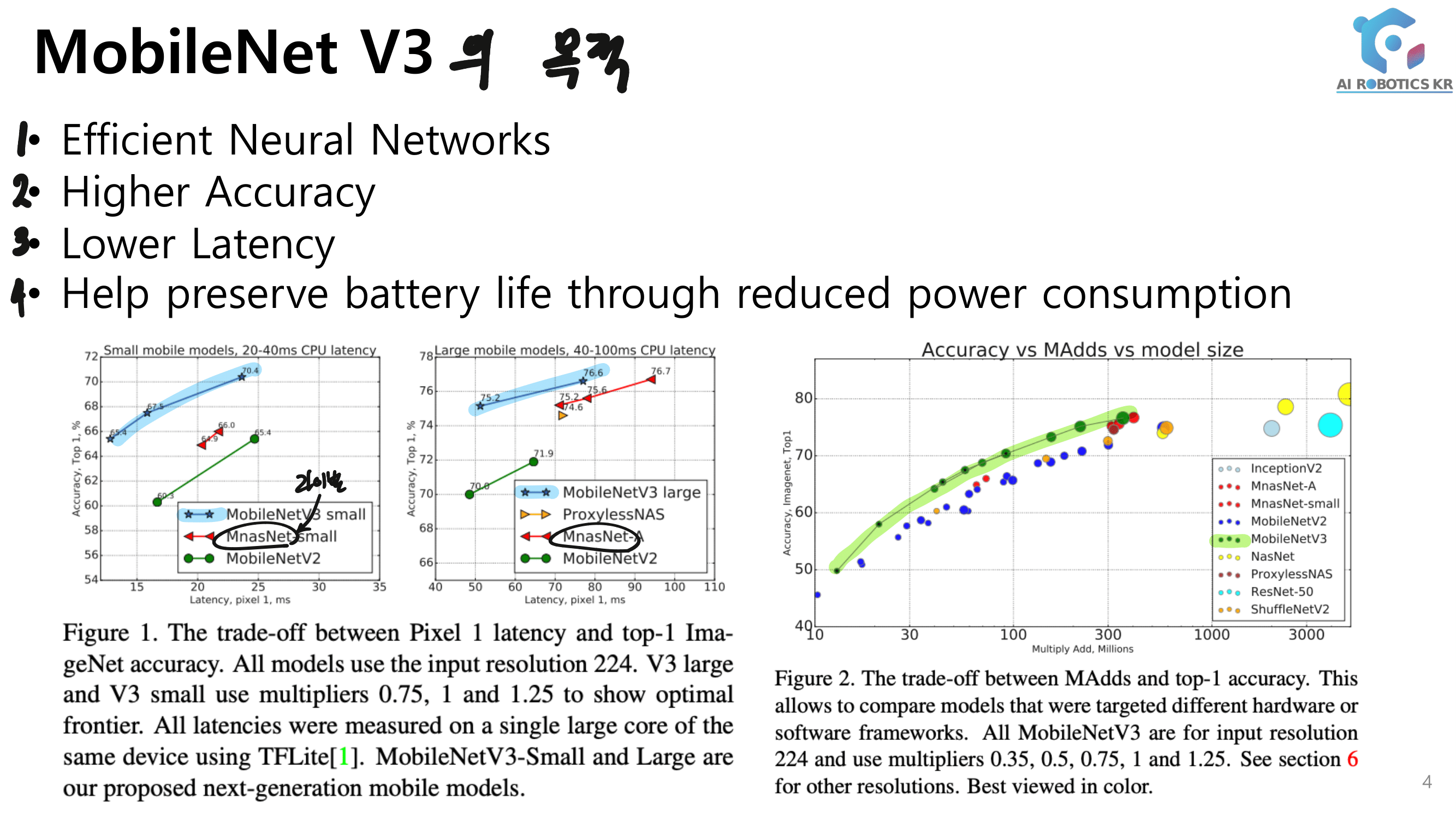
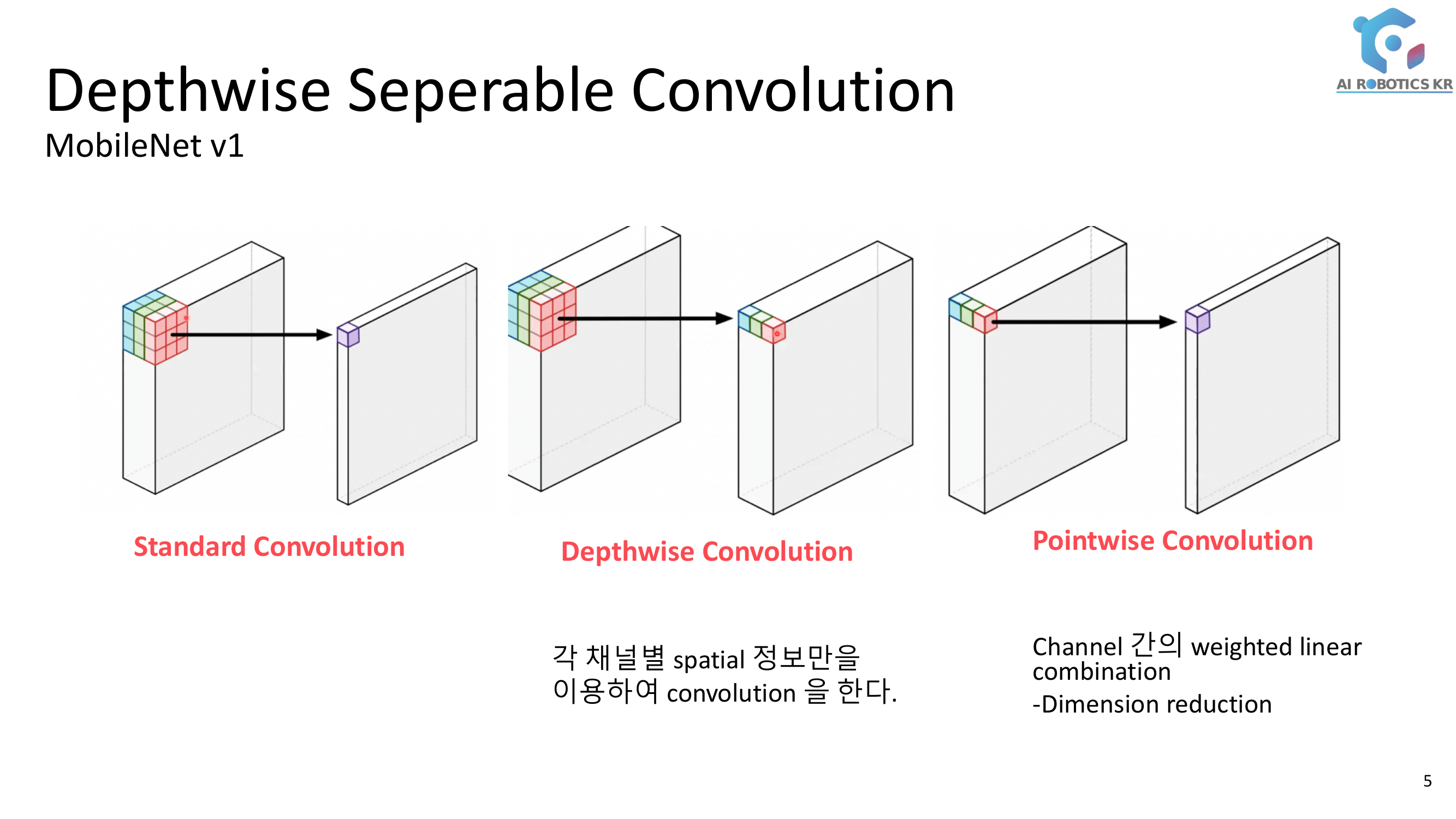
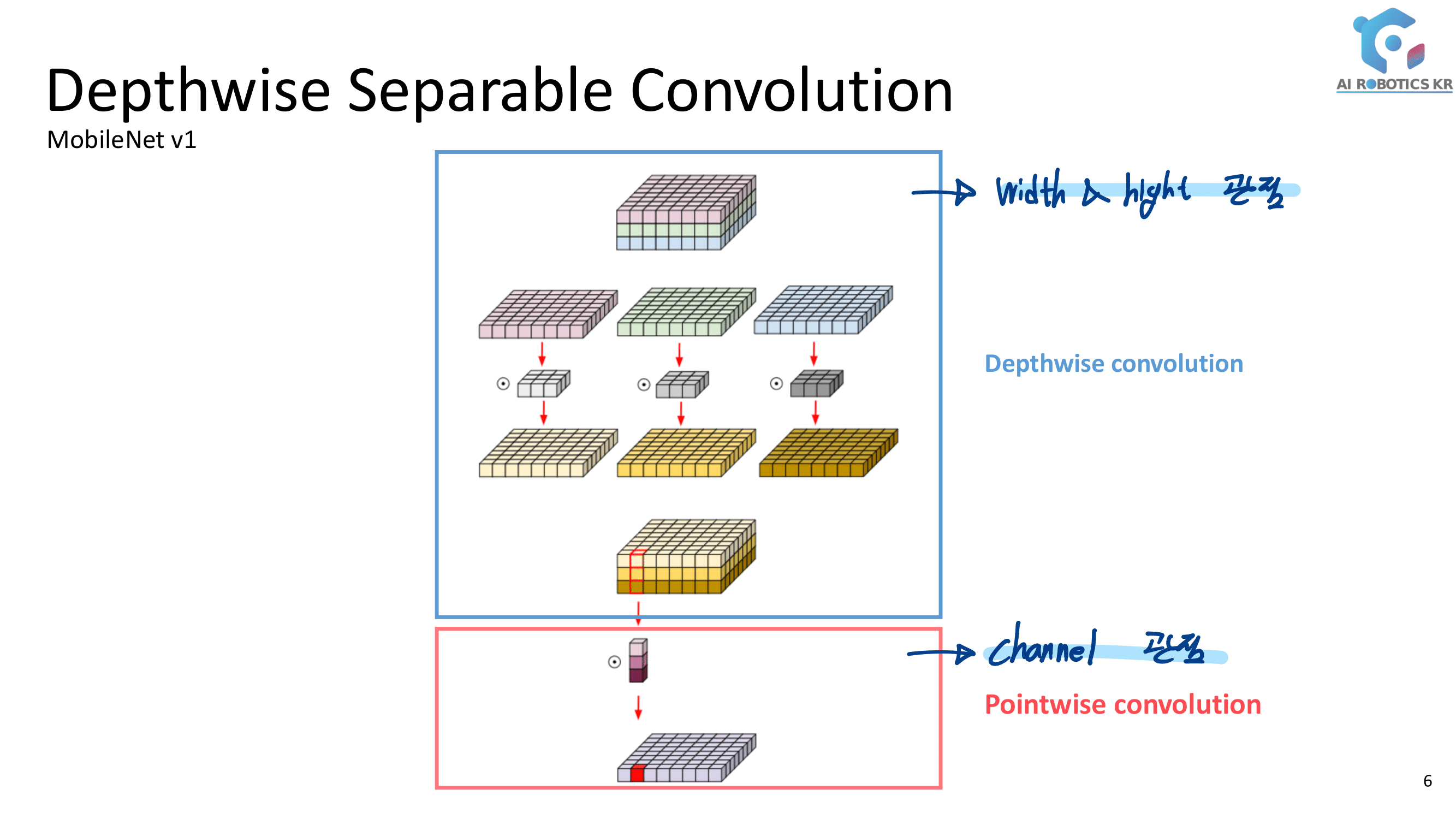





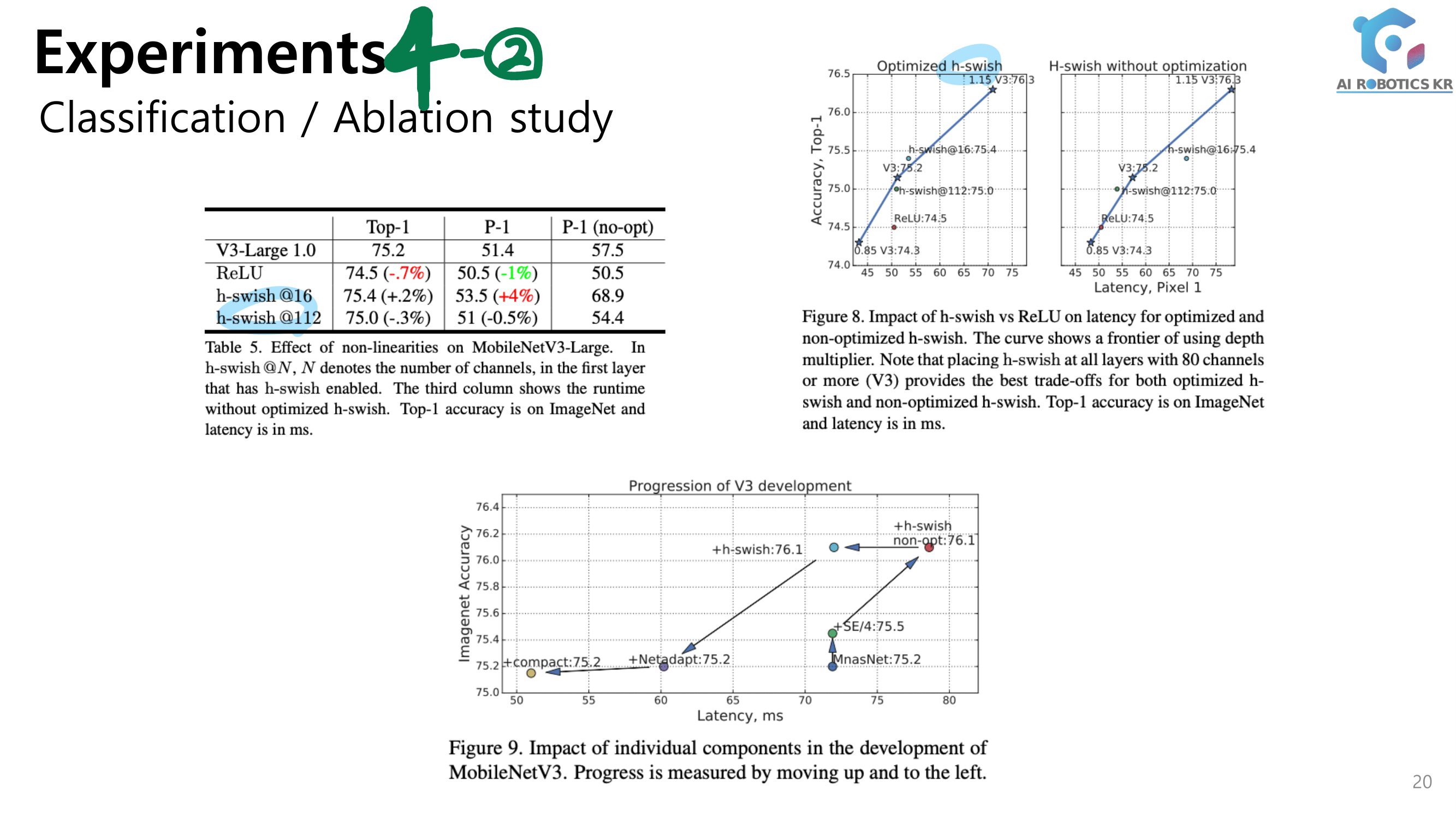
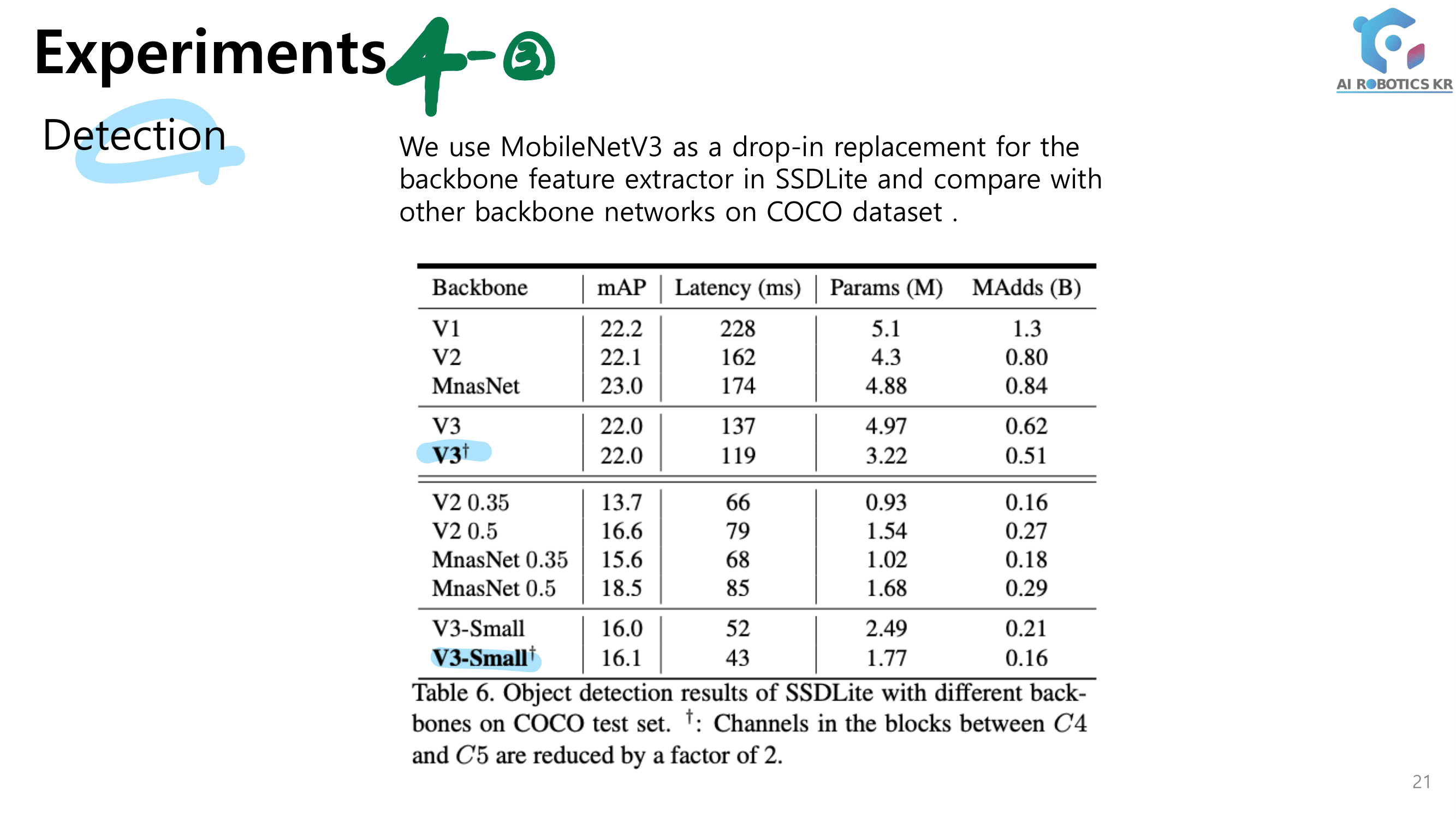
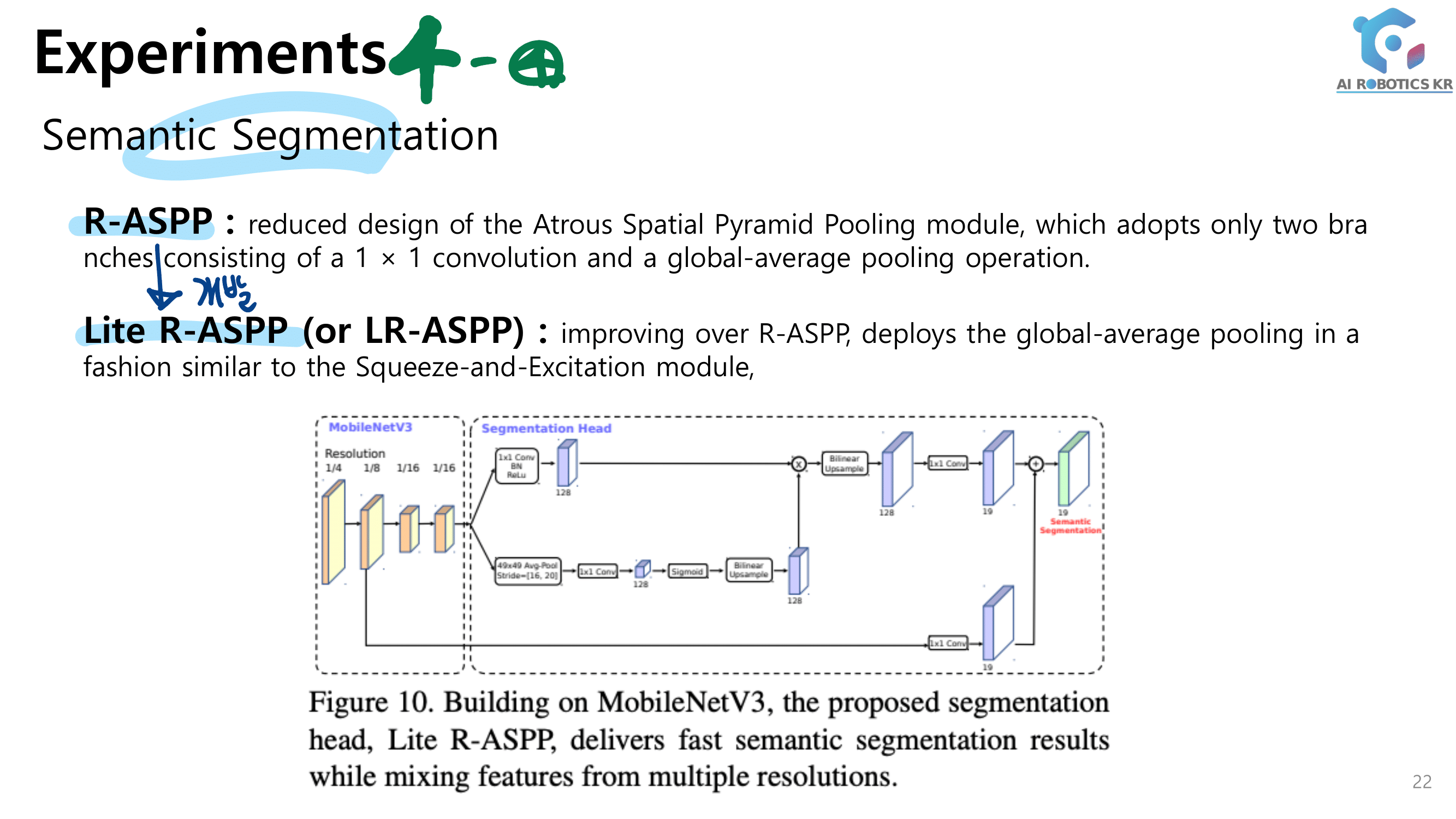



3. DenseNet
AlexNet, ZFNet(필터 사이즈 및 갯수 등 하이퍼파라미터의 중요성 부각)
VGG : Small Filters, Deeper networks -> 3X3 여러개를 사용하는 것의 파라메터 갯수 관점에서 더 효율적.
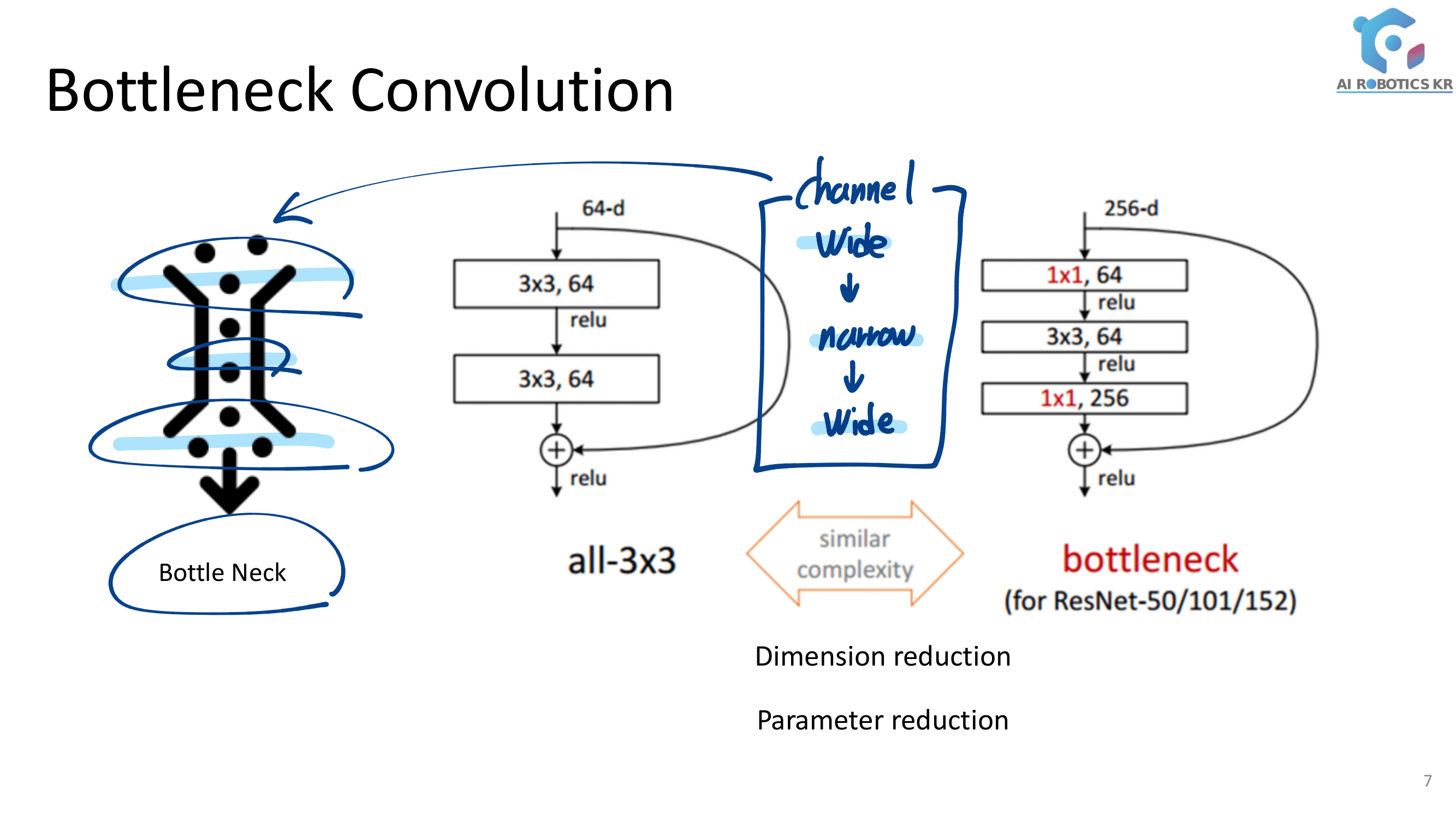
Inception = GoogleNet : FC Layer를 줄이기 위해 노력. 다양한 conv를 적용하고 나중에 Concat. 이때 큰 Filter size conv를 하기 전에 1x1으로 channel reduction (= BottleNet Layer)을 해준다.
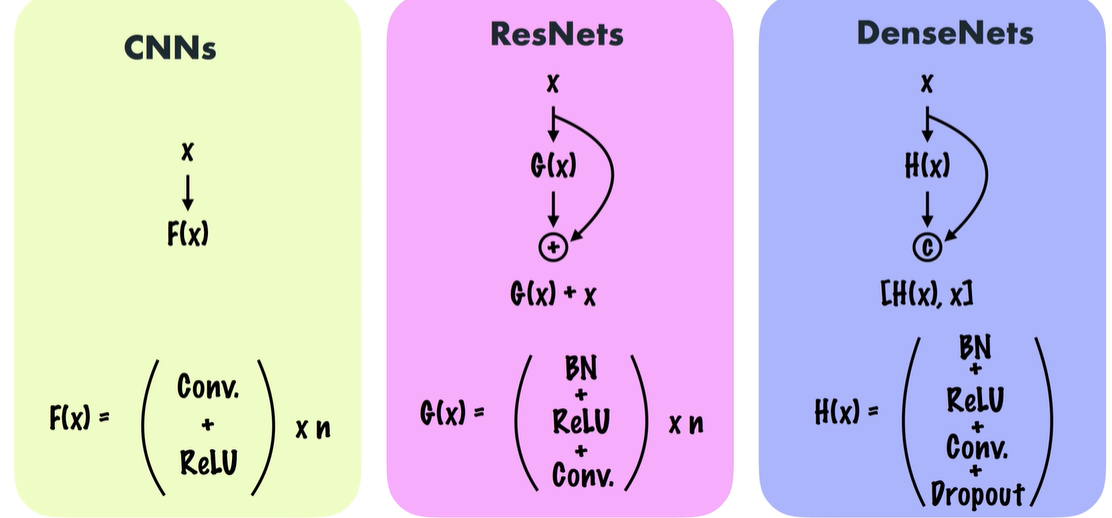
ResNet : Residual Connnetion(=Skip Connection + Element-wise addition). Layer가 깊다고 무조건 좋은게 아니었다. Gradient Vanishing문제! -> ResNeXt = ResNet + Inception
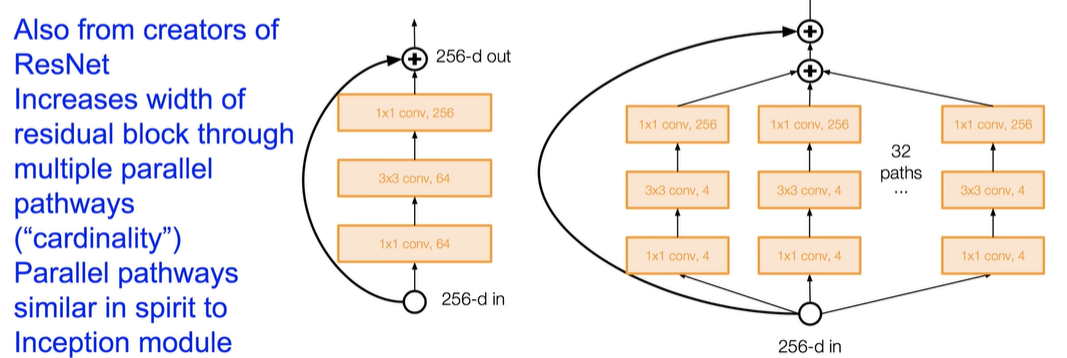
ResNet의 Improving 형태 -> Srochastic Depth : 오른쪽 그림의 회색과 같이, 랜덤하게 일부 Layer를 끄고 학습일 시킨다. 더 좋은 결과가 나오더라

Densely Connected Convolutional Networks
ResNet 처럼 다음단만 연결하지 말고, 모조리 다 연결해보자.
Element-wise addition 하지 말고, Channel-wise Concatenation 하자!
Dense And Slim하다! 왜냐면 Channel을 크게 가져갈 필요없기 때문이다. Layer를 통과할 때마다 k(=12)개씩 Channel 수가 증가하도록만 만들어도 충분히 학습이 잘 되니까.

또는 아래와 같이 BottleNetck Layer를 사용하면 아래와 같다.

위의 모든 연산을, 하나의 Layer를 통과한 것으로 본다면, 모든 연산후에는 항상 k개의 channel이 생기게 만든다. (어차피 나중에 (l = 이전에 통과한 Layer 갯수) l x k 개의 Channel과 합쳐야 하므로 새로 생긴 k가 너무 크지 않도록 만든다. 여기서 k는 12를 사용했다고 함)
위의 작업들을 모듈화로 하여, 여러번 반복함으로써 다음과 같은 전체 그림을 만들 수 있다. 논문에서는 일반적으로 DenseBlock을 3개 정도 사용하였다.
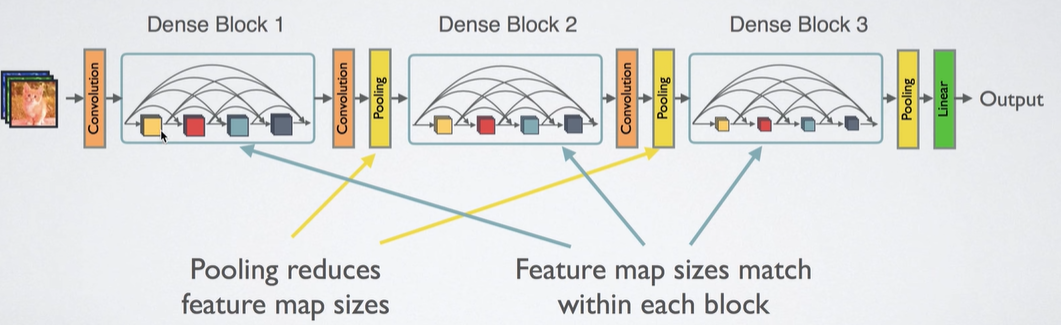
장점
- 학습이 잘된다. Error Signal의 전달 = Backpropa가 잘된다.
- 기존의 것들은 중간 Layer의 Channel의 size가 매우 커야 학습이 잘 됐는데, 우리의 Channel은 작은값 k를 이용해서 최대 lxk개의 Channel만을 가지도록 만들었다.
- 그마큼 사용되는 # parameters 또한 줄어진다. O(C*C(중간 Layer의 channel 갯수)) » O(L*k*k)
- 아래의 그림처럼 모든 Layer의 Feature들을 사용한다. 아래 그림의 ‘별’은 Complex정도를 의미한다. 원래 다른 network는 Classifier에서 가장 마지막 별5개짜리 Layer만을 이용한다. 하지만 우리의 Classifier는 지금까지의 모든 Layer결과를 한꺼번에 이용한다. 따라서 굉장히 효율성이 좋다.
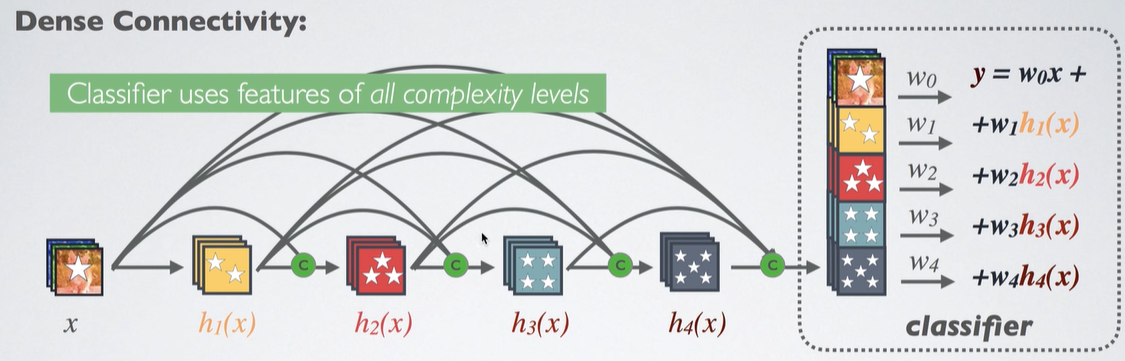
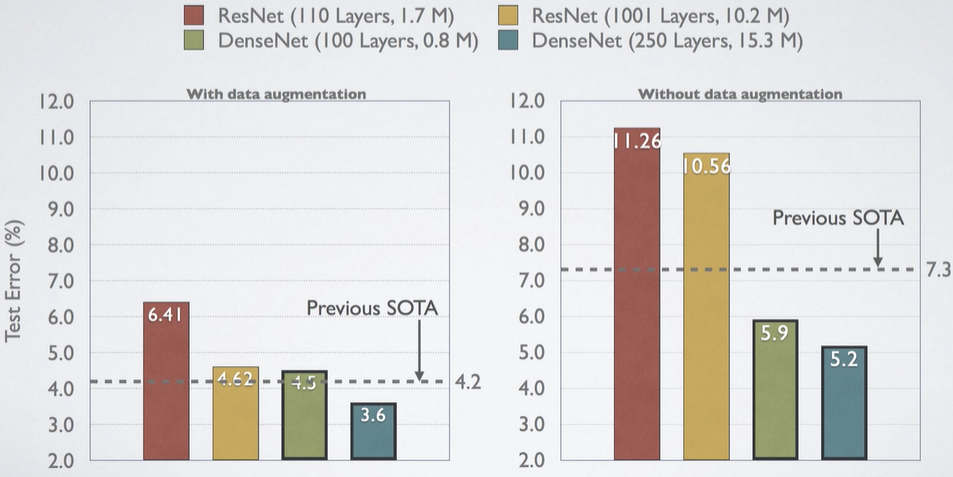
결과
논문에 없는 추가 내용
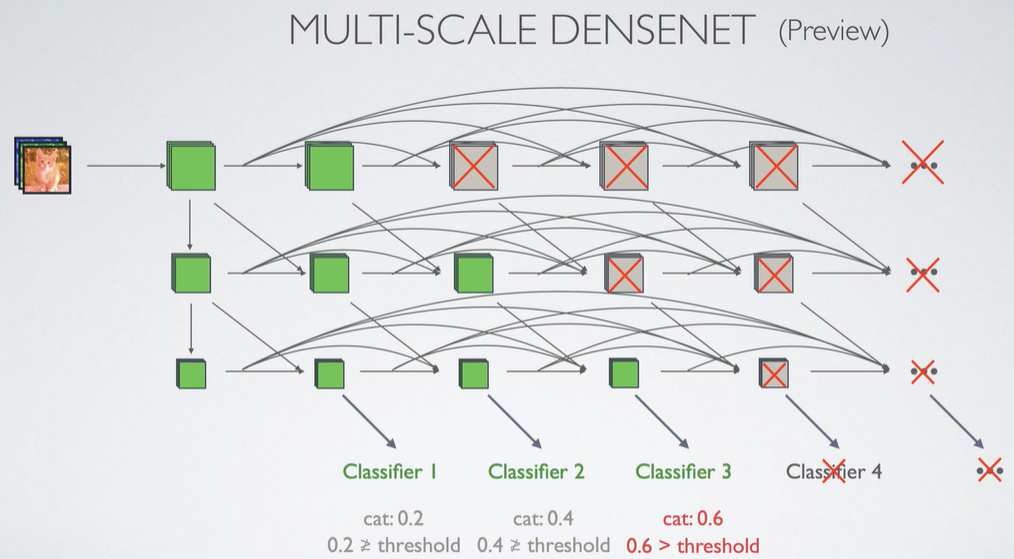
- Easy Example은 앞의 Classifier1에서 처리하고, Hard Example은 뒤의 Classifier3에서 처리하도록 만들면, 더 빠른 예측이 가능하다. 그니까.. Classifier1에서 일정 이상의 값이 나온 것은 예측값 그대로 결과에 사용하고 거기서 Stop.(빨리 끝. 전체 평균 처리 속도 상승) 반대로 모든 클래스에서 일정 threshold값 이상이 나오지 않는다면, 다음 Classifier에서 분류를 다시 해보는 작업을 수행한다.
- 전체 수식 정리